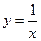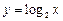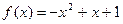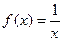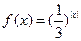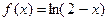题目内容
设函数f(x)=lg(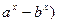 (a>1>b>0),当a,b满足什么关系时,f(x)在(1,+∞)上恒取正值?
(a>1>b>0),当a,b满足什么关系时,f(x)在(1,+∞)上恒取正值?
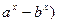 (a>1>b>0),当a,b满足什么关系时,f(x)在(1,+∞)上恒取正值?
(a>1>b>0),当a,b满足什么关系时,f(x)在(1,+∞)上恒取正值?a-b≥1
由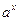 -
- >0得
>0得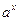 >
> ,由a>1>b>0得x>0,所以f(x)的定义域为(0,+∞)。可以证明(利用定义或导数法)f(x) 在(0,+∞)是增函数,所以x>1时,f(x) >f(1)。要使函数f(x)在(1,+∞)上恒取正值,只要f(1)≥0,即a-b≥1。
,由a>1>b>0得x>0,所以f(x)的定义域为(0,+∞)。可以证明(利用定义或导数法)f(x) 在(0,+∞)是增函数,所以x>1时,f(x) >f(1)。要使函数f(x)在(1,+∞)上恒取正值,只要f(1)≥0,即a-b≥1。
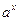 -
- >0得
>0得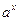 >
> ,由a>1>b>0得x>0,所以f(x)的定义域为(0,+∞)。可以证明(利用定义或导数法)f(x) 在(0,+∞)是增函数,所以x>1时,f(x) >f(1)。要使函数f(x)在(1,+∞)上恒取正值,只要f(1)≥0,即a-b≥1。
,由a>1>b>0得x>0,所以f(x)的定义域为(0,+∞)。可以证明(利用定义或导数法)f(x) 在(0,+∞)是增函数,所以x>1时,f(x) >f(1)。要使函数f(x)在(1,+∞)上恒取正值,只要f(1)≥0,即a-b≥1。
练习册系列答案
相关题目
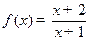 在
在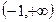 上是减函数。
上是减函数。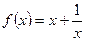
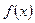 在区间
在区间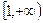 上为增函数
上为增函数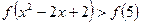
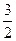
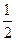


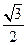
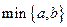 表示a,b两数中的最小值。若函数
表示a,b两数中的最小值。若函数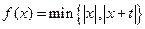 的图像关于直线x=
的图像关于直线x=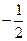 对称,则t的值为 ( )
对称,则t的值为 ( )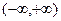 上是减函数,则实数a的取值范围是 ( )
上是减函数,则实数a的取值范围是 ( )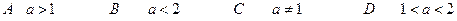
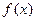 是定义在
是定义在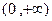 上的增函数,且对一切
上的增函数,且对一切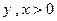 满足
满足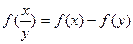
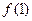
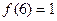 ,解不等式
,解不等式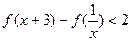
 上是增函数的是( )
上是增函数的是( )