题目内容
6.二次函数y=x2-3x-4的定义域为[0,m],最大值为-4,最小值为-$\frac{25}{4}$,则m的范围是[$\frac{3}{2}$,3].分析 根据函数的函数值f($\frac{3}{2}$)=-$\frac{25}{4}$,f(0)=-4,结合函数的图象即可求解.
解答 解:画出函数的图象,如图示: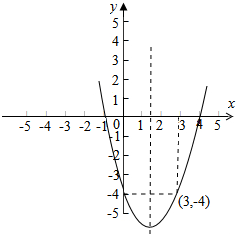
∵f(x)=x2-3x-4=(x-$\frac{3}{2}$)2-$\frac{25}{4}$,
∴f($\frac{3}{2}$)=-$\frac{25}{4}$,又f(0)=-4,
故由二次函数图象可知:
m的值最小为$\frac{3}{2}$;最大为3.
m的取值范围是:$\frac{3}{2}$≤m≤3.
故答案[$\frac{3}{2}$,3].
点评 本题考查了二次函数的性质,特别是利用抛物线的对称特点进行解题,属于基础题.

练习册系列答案
相关题目
17.2${\;}^{lo{g}_{4}3}$等于( )
| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{1}{3}$ |
14.已知非零向量$\overrightarrow{a}$、$\overrightarrow{b}$满足$\overrightarrow{a}$⊥$\overrightarrow{b}$,则函数f(x)=($\overrightarrow{a}$x+$\overrightarrow{b}$)2•x2(x∈R)是( )
| A. | 既是奇函数又是偶函数 | B. | 非奇非偶函数 | ||
| C. | 偶函数 | D. | 奇函数 |
16.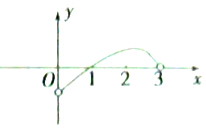 已知定义在区间(0,3)上的函数f(x)的图象如图所示,若$\overrightarrow{a}$=(f(x),0),$\overrightarrow{b}$=(cosx,1),则不等式$\overrightarrow{a}$•$\overrightarrow{b}$<0的解集是( )
已知定义在区间(0,3)上的函数f(x)的图象如图所示,若$\overrightarrow{a}$=(f(x),0),$\overrightarrow{b}$=(cosx,1),则不等式$\overrightarrow{a}$•$\overrightarrow{b}$<0的解集是( )
 已知定义在区间(0,3)上的函数f(x)的图象如图所示,若$\overrightarrow{a}$=(f(x),0),$\overrightarrow{b}$=(cosx,1),则不等式$\overrightarrow{a}$•$\overrightarrow{b}$<0的解集是( )
已知定义在区间(0,3)上的函数f(x)的图象如图所示,若$\overrightarrow{a}$=(f(x),0),$\overrightarrow{b}$=(cosx,1),则不等式$\overrightarrow{a}$•$\overrightarrow{b}$<0的解集是( )| A. | (0,1) | B. | (0,1] | C. | (0,1)∪($\frac{π}{2}$,3) | D. | (0,1]∪($\frac{π}{2}$,3) |