题目内容
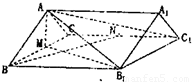
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,,AB=AD=A1B=2CD,侧面A1ADD1为正方形.(1)求直线A1A与底面ABCD所成角的大小;
(2)求二面角C-A1B-A正切值的大小;
(3)在棱C1C上是否存在一点P,使得 D1P∥平面A1BC,若存在,试说明点P的位置;若不存在,请说明理由.

【答案】分析:(1)做出辅助线,根据面面垂直得到线线垂直,进而得到线面垂直,得到∠A1AB为直线A1A与平面ABCD所成的角.求出结果
(2)做出辅助线,过O作OH⊥A1B,垂足为H,连接CH.根据OC∥DA,DA⊥平面AA1B1B,得到CO⊥平面AA1B1B.得到∠CHO为二面角C-A1B-A的平面角,在三角形求出角的正切值
(3)结论是存在.当点P为棱C1C中点时,D1P∥平面A1BC.根据线面平行的判定定理整出结论.
解答:解:(1)取AB中点O,连接A1O.设AB=a.∵AD⊥AA1,AD⊥AB,AA1∩AB=A,
∴AD⊥平面AA1B1B,AD?而ABCD∴平面AA1B1B⊥平面ABCD.
∵AB=AA1=A1B=a,∴A1O⊥AB,∴A1O⊥平面ABCD.
∴∠A1AB为直线A1A与平面ABCD所成的角.
∵∠A1AB=60°,∴直线A1A与平面ABCD所成角的大小为60°
(2)过O作OH⊥A1B,垂足为H,连接CH.∵OC∥DA,DA⊥平面AA1B1B,
∴CO⊥平面AA1B1B.
∵OH⊥A1B,∴CH⊥A1B.∴∠CHO为二面角C-A1B-A的平面角.
在正△A1AB中, ,
,
在Rt△COH中,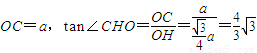 .
.
∴二面角C-A1B-A正切值的大小为 .
.
(3)存在.当点P为棱C1C中点时,D1P∥平面A1BC.
证明如下
延长D1P与DC交于Q,连接BQ,∵点P为棱C1C中点,
∴PC为△D1DQ的中位线.∴QC=DC.
由条件,得四边形ABQD为正方形.
∴BQ=AD=A1D1,且BQ∥AD∥A1D1.
则四边形A1BQD1是平行四边形.
∴D1P∥A1B.∵D1P?平面A1BC.A1B?平面A1BC.
∴D1P∥平面A1BC.
点评:本题主要考查了线面平行的判定,以及利用空间向量的方法求解二面角等有关知识,同时考查了空间想象能力、转化与划归的思想,属于中档题.
(2)做出辅助线,过O作OH⊥A1B,垂足为H,连接CH.根据OC∥DA,DA⊥平面AA1B1B,得到CO⊥平面AA1B1B.得到∠CHO为二面角C-A1B-A的平面角,在三角形求出角的正切值
(3)结论是存在.当点P为棱C1C中点时,D1P∥平面A1BC.根据线面平行的判定定理整出结论.
解答:解:(1)取AB中点O,连接A1O.设AB=a.∵AD⊥AA1,AD⊥AB,AA1∩AB=A,
∴AD⊥平面AA1B1B,AD?而ABCD∴平面AA1B1B⊥平面ABCD.
∵AB=AA1=A1B=a,∴A1O⊥AB,∴A1O⊥平面ABCD.
∴∠A1AB为直线A1A与平面ABCD所成的角.
∵∠A1AB=60°,∴直线A1A与平面ABCD所成角的大小为60°
(2)过O作OH⊥A1B,垂足为H,连接CH.∵OC∥DA,DA⊥平面AA1B1B,
∴CO⊥平面AA1B1B.
∵OH⊥A1B,∴CH⊥A1B.∴∠CHO为二面角C-A1B-A的平面角.
在正△A1AB中,
 ,
,在Rt△COH中,
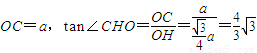 .
.∴二面角C-A1B-A正切值的大小为
 .
.(3)存在.当点P为棱C1C中点时,D1P∥平面A1BC.
证明如下
延长D1P与DC交于Q,连接BQ,∵点P为棱C1C中点,
∴PC为△D1DQ的中位线.∴QC=DC.
由条件,得四边形ABQD为正方形.
∴BQ=AD=A1D1,且BQ∥AD∥A1D1.
则四边形A1BQD1是平行四边形.
∴D1P∥A1B.∵D1P?平面A1BC.A1B?平面A1BC.
∴D1P∥平面A1BC.
点评:本题主要考查了线面平行的判定,以及利用空间向量的方法求解二面角等有关知识,同时考查了空间想象能力、转化与划归的思想,属于中档题.

练习册系列答案
相关题目
 如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.
如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点. (2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.
(2007•无锡二模)如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD为直角梯形,AB∥CD,AB⊥AD,AB=AD=A1B=2CD,侧面A1ADD1为正方形.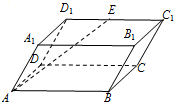 如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,∠BAA1=60°,E为棱C1D1的中点,则