题目内容
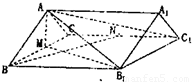
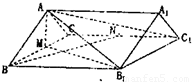
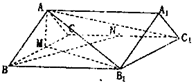 如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.
如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.(1)求证:BN⊥AB1;
(2)求四棱锥A-MB1C1C与三棱柱ABC-A1B1C1的体积比.
分析:(1)在正方形BB1C1C中,利用三角形全等证出BN⊥B1M,再利用直三棱柱的性质和面面垂直的判定与性质,得到BN⊥AM,从而得到BN⊥平面AB1M,再由AB1?平面AB1M,得BN⊥AB1;
(2)利用勾股定理,算出四棱锥A-MB1C1C的高为AM=3,结合四边形MB1C1C的面积,可算出四棱锥A-MB1C1C的体积为48;而由已知条件易算出三棱柱ABC-A1B1C1的体积为96,由此可得四棱锥A-MB1C1C与三棱柱ABC-A1B1C1的体积比.
(2)利用勾股定理,算出四棱锥A-MB1C1C的高为AM=3,结合四边形MB1C1C的面积,可算出四棱锥A-MB1C1C的体积为48;而由已知条件易算出三棱柱ABC-A1B1C1的体积为96,由此可得四棱锥A-MB1C1C与三棱柱ABC-A1B1C1的体积比.
解答:解:(1)∵直棱柱ABC-A1B1C1中,BC=BB1,
∴侧面BB1C1C为正方形
∵M,N分别为BC,CC1的中点,
∴Rt△BCN≌Rt△B1BM,得∠CBN=∠BB1M=90°-∠NBB1,
由此可得∠NBB1+∠BB1M=90°,得BN⊥B1M
∵直棱柱ABC-A1B1C1中,B1B⊥平面ABC,B1B?平面BB1C1C
∴平面ABC⊥平面BB1C1C
∵△ABC中,AB=AC=5,M为BC中点,∴AM⊥BC
∵平面ABC∩平面BB1C1C=BC,AM?平面ABC
∴AM⊥平面BB1C1C,结合BN?平面BB1C1C,得BN⊥AM
∵AM、B1N是平面AB1M内的相交直线
∴BN⊥平面AB1M,再由AB1?平面AB1M,得BN⊥AB1;
(2)∵AB=5,MB=
BC=4,∴AM=
=3
∴四棱锥A-MB1C1C的体积:VA-MB1C1C=
S四边形MB1C1C•AM=
×(82-
×8×4)=48
又∵三棱柱ABC-A1B1C1的体积V三棱柱ABC-A1B1C1=S△ABC•BB1=
×8×3×8=96
∴四棱锥A-MB1C1C与三棱柱ABC-A1B1C1的体积比为48:96=1:2.
∴侧面BB1C1C为正方形
∵M,N分别为BC,CC1的中点,
∴Rt△BCN≌Rt△B1BM,得∠CBN=∠BB1M=90°-∠NBB1,
由此可得∠NBB1+∠BB1M=90°,得BN⊥B1M
∵直棱柱ABC-A1B1C1中,B1B⊥平面ABC,B1B?平面BB1C1C
∴平面ABC⊥平面BB1C1C
∵△ABC中,AB=AC=5,M为BC中点,∴AM⊥BC
∵平面ABC∩平面BB1C1C=BC,AM?平面ABC
∴AM⊥平面BB1C1C,结合BN?平面BB1C1C,得BN⊥AM
∵AM、B1N是平面AB1M内的相交直线
∴BN⊥平面AB1M,再由AB1?平面AB1M,得BN⊥AB1;
(2)∵AB=5,MB=
| 1 |
| 2 |
| AB2-BM2 |
∴四棱锥A-MB1C1C的体积:VA-MB1C1C=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
又∵三棱柱ABC-A1B1C1的体积V三棱柱ABC-A1B1C1=S△ABC•BB1=
| 1 |
| 2 |
∴四棱锥A-MB1C1C与三棱柱ABC-A1B1C1的体积比为48:96=1:2.
点评:本题给出直三棱柱,求证异面直线相互垂直并求两个几何体的体积之比,着重考查了空间线面垂直、面面垂直的判定与性质和柱体、锥体的体积公式等知识,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4,E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4,E、F分别是棱CC1、AB中点.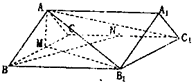 如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.
如图,已知直棱柱ABC-A1B1C1中,AB=AC=5,BC=BB1=8,M,N分别为棱BC,CC1的中点.