题目内容
【题目】有三个球,第一个球内切于正方体的六个面,第二个球与这个正方体的各条棱相切,第三个球过这个正方体的各个顶点,若正方体的棱长为![]() ,求这三个球的表面积.
,求这三个球的表面积.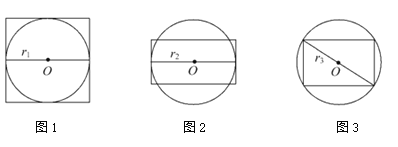
【答案】(1)![]() ,(2)
,(2)![]() ,(3)
,(3)![]() .
.
【解析】试题分析:(1))正方体的内切球球心是正方体的中心,切点是六个面(正方形)的中心,据此可求半径、面积;(2)球与正方体各棱的切点在每条棱的中点,过球心作正方体的对角面得截面,对棱之间距离就是球直径;(3)正方体的各个顶点在球面上, 正方体的对角线就是球的直径.
试题解析:(1)正方体的内切球球心是正方体的中心,切点是六个面(正方形)的中心,经过四个切点及球心作截面,如图(1),所以有2r1=a,r1=![]() ,所以S1=4π
,所以S1=4π![]() =πa2.
=πa2.
(2)球与正方体各棱的切点在每条棱的中点,过球心作正方体的对角面得截面,如图(2),所以有2r2=![]() a,r2=
a,r2=![]() a,所以S2=4π
a,所以S2=4π![]() =2πa2.
=2πa2.
(3)正方体的各个顶点在球面上,过球心作正方体的对角面得截面,如图(3),所以有2r3=![]() a,r3=
a,r3=![]() a,所以S3=4π
a,所以S3=4π![]() =3πa2.
=3πa2.

【题目】某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
年份200 | 0 | 1 | 2 | 3 | 4 |
人口数 | 5 | 7 | 8 | 11 | 19 |
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(3)据此估计2005年该城市人口总数.
参考公式: 用最小二乘法求线性回归方程系数公式 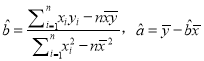
【题目】(本小题12分)甲、乙两位学生参加数学竞赛培训,在培训期间,他们参加的5项预赛成绩记录如下:
甲 | 82 | 82 | 79 | 95 | 87 |
乙 | 95 | 75 | 80 | 90 | 85 |
(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;
(2)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?说明理由.