题目内容
(本小题满分12分)
已知函数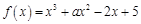 .
.
(1)若函数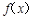 在(
在(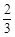 ,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
(2)是否存在正整数a,使得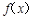 在(
在(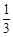 ,
,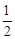 )上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
)上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
已知函数
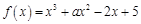 .
.(1)若函数
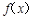 在(
在(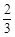 ,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;(2)是否存在正整数a,使得
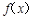 在(
在(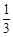 ,
,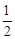 )上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
)上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.(1)a=-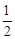 .(2)a=2.
.(2)a=2.
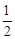 .(2)a=2.
.(2)a=2. 本试题主要是考查了导数在研究函数中的运用。
(1)先求解导数分析单调区间,,然后得到实数a的值。
(2)根据在区间上不增不见,因此说明导数为零方程有解,分析可知参数a的值。
解 (1)∵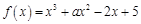 在(
在(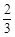 ,1)上单调递减,在(1,+∞)上单调递增,
,1)上单调递减,在(1,+∞)上单调递增,
∴f′(x)=3x2+2ax-2, ……………………………………2分
f′(1)=0,∴a=-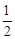 .……………………………6分
.……………………………6分
(2)令f′(x)=3x2+2ax-2=0.………15分
∵a是正整数,∴a=2.………………………16分
(1)先求解导数分析单调区间,,然后得到实数a的值。
(2)根据在区间上不增不见,因此说明导数为零方程有解,分析可知参数a的值。
解 (1)∵
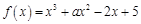 在(
在(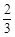 ,1)上单调递减,在(1,+∞)上单调递增,
,1)上单调递减,在(1,+∞)上单调递增,∴f′(x)=3x2+2ax-2, ……………………………………2分
f′(1)=0,∴a=-
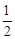 .……………………………6分
.……………………………6分(2)令f′(x)=3x2+2ax-2=0.………15分
∵a是正整数,∴a=2.………………………16分

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
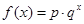 ;②
;②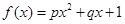 ;③
;③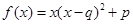 .(以上三式中、
.(以上三式中、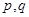 均为常数,且
均为常数,且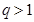 )
)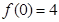 ,
,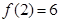 ,求出所选函数
,求出所选函数 的解析式(注:函数定义域是
的解析式(注:函数定义域是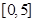 .其中
.其中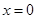 表示8月1日,
表示8月1日,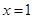 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);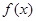 的定义域为
的定义域为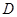 ,若存在非零实数
,若存在非零实数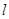 使得对于任意
使得对于任意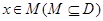 ,有
,有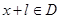 ,且
,且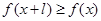 ,则称
,则称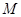 上的
上的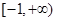 的函数
的函数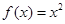 为
为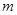 高调函数,那么实数
高调函数,那么实数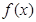 是定义在
是定义在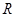 上的奇函数,且当
上的奇函数,且当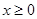 时,
时,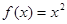 ,若对任意的
,若对任意的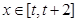 ,不等式
,不等式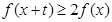 恒成立,则实数
恒成立,则实数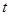 的取值范围为( )
的取值范围为( )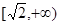
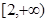
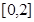
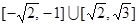
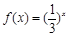 , 其反函数为
, 其反函数为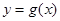
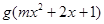 的定义域为
的定义域为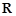 ,求实数
,求实数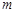 的取值范围;
的取值范围;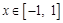 时,求函数
时,求函数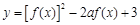 的最小值
的最小值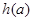 ;
;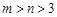 ,使得函数
,使得函数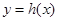 的定义域为
的定义域为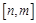 ,值域为
,值域为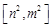 ,若存在,求出
,若存在,求出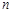 的值;若不存在,则说明理由.
的值;若不存在,则说明理由.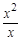 -1
-1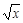 )4
)4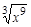
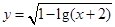 的定义域为
的定义域为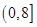
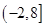
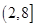
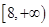
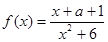 为奇函数,则实数
为奇函数,则实数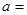 ___________
___________