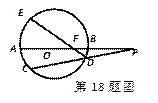题目内容
(本小题满分10分)选修4—1:几何证明选讲
如图,AB是⊙O的直径,弦BD、CA的延长线相交于
点E,EF垂直BA的延长线于点F. 求证:
(Ⅰ)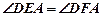 ;
;
(Ⅱ)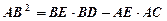

证明:(Ⅰ)连结AD因为AB为圆的直径,所以∠ADB=90°,又EF⊥AB,∠EFA=90°则A、D、E、F四点共圆(4分)∴∠DEA=∠DFA (5分)
(Ⅱ)由(Ⅰ)知,BD•BE=BA•BF(6分),又△ABC∽△AEF∴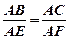
即:AB•AF=AE•AC(8分)∴ BE•BD-AE•AC ="BA•BF-AB•AF=AB(BF-AF)=AB2 " (10分)
解析

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
直线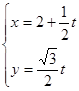 (
( 为参数)被曲线
为参数)被曲线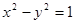 截得的弦长是( )
截得的弦长是( )
| | A. | 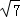 | B. | 2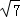 | C. | 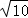 | D. | 2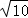 |
曲线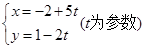 与坐标轴的交点是( )
与坐标轴的交点是( )
A.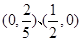 | B.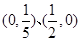 |
C.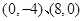 | D.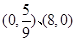 |

 ;
; 中,
中, ,
,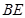 平分
平分 交
交 于点
于点 ,点
,点 在
在 上,
上, .
.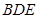 的外接圆的切线;
的外接圆的切线;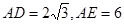 ,求
,求 的长.
的长.
 •BD
•BD 于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转
于点A,割线PBC经过圆心O,OB=PB=1,OA绕点O逆时针旋转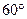 到O D.
到O D.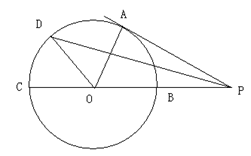
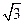 的线段?若有,指出该线段;若没有,说明理由.
的线段?若有,指出该线段;若没有,说明理由.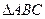 是等腰直角三角形,
是等腰直角三角形,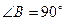 ,
,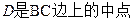 ,
,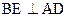 ,延长
,延长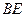 交
交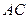 于
于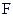 ,连接
,连接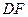 ,求证:
,求证: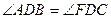

 如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,A为弧CE的重点,DE交AB于点F,且AB=2BP=4,求PF的长度。