题目内容
已知曲线方程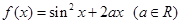 ,若对任意实数
,若对任意实数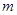 ,直线
,直线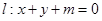
都不是曲线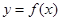 的切线,则
的切线,则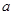 的取值范围是
的取值范围是
(-∞,-1)∪(0,+∞)
解析试题分析:若存在实数m,使直线l是曲线y=f(x)的切线,∵f′(x)=2sinxcosx+2a=sin2x+2a,∴方程sin2x+2a=-1有解,∴-1≤a≤0,故所求a的取值范围是(-∞,-1)∪(0,+∞)。
考点:导数的几何意义,方程的解。
点评:中档题,利用导数的几何意义,假定切线存在,则导函数值等于切线的斜率,建立方程,确定得到参数的范围。

练习册系列答案
相关题目
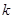 ,使得对定义域
,使得对定义域 内的任意两个
内的任意两个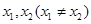 ,均有
,均有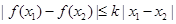 成立,则称函数
成立,则称函数 在定义域
在定义域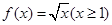 满足利普希茨条件,则常数
满足利普希茨条件,则常数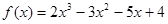 的导数
的导数 ,
,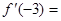
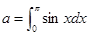 ,则曲线
,则曲线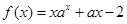 在点
在点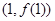 处的切线的斜率为__________.
处的切线的斜率为__________.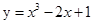 在点(1,f(x))处的切线方程为
在点(1,f(x))处的切线方程为  在(
在(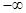 ,+
,+ )内有意义.对于给定的正数K,已知函数
)内有意义.对于给定的正数K,已知函数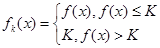 ,取函数
,取函数 =
= .若对任意的
.若对任意的
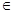 (
(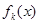 =
=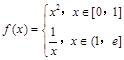 (其中
(其中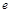 为自然对数的底数),则
为自然对数的底数),则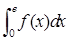 = .
= . 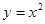 与
与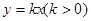 的图像所围成的图形的面积为
的图像所围成的图形的面积为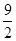 ,则
,则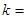 .
.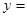
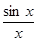 的导函数
的导函数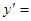 .
.