题目内容
将锐角为60°边长为a的菱形ABCD沿最长对角线BD折成60°的二面角,则AC与BD之间的距离是( )A.
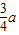
B.
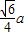
C.
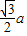
D.

【答案】分析:设E、F分别是中点,根据菱形的性质可得:BD⊥平面ACE,所以BD⊥EF.又因为EF⊥AC,可得折后两条对角线AC、BD之间的距离为EF的长,再利用解三角形的有关知识求出EF的长即可.
解答:解:设E、F分别是中点,由题可得:∠AEC=60°,
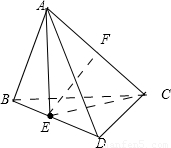
因为AE⊥DB,CE⊥BD,所以BD⊥平面ACE,所以BD⊥EF.
又因为AE=CE,
所以EF⊥AC.
所以折后两条对角线AC、BD之间的距离为EF的长,
在△AEC中,∠AEC=60°,AE=EC= a,
a,
所以EF=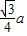 .
.
故选D.
点评:本题主要考查二面角问题,解决此类问题一般先作出二面角的平面角,再通过解∠AEC所在的三角形求得两条异面直线之间的距离.
解答:解:设E、F分别是中点,由题可得:∠AEC=60°,

因为AE⊥DB,CE⊥BD,所以BD⊥平面ACE,所以BD⊥EF.
又因为AE=CE,
所以EF⊥AC.
所以折后两条对角线AC、BD之间的距离为EF的长,
在△AEC中,∠AEC=60°,AE=EC=
 a,
a,所以EF=
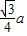 .
.故选D.
点评:本题主要考查二面角问题,解决此类问题一般先作出二面角的平面角,再通过解∠AEC所在的三角形求得两条异面直线之间的距离.

练习册系列答案
相关题目
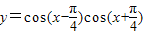 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为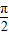 ;
;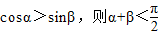 ;
;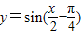 的图象,只需将
的图象,只需将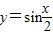 的图象向右平移
的图象向右平移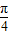 个单位.
个单位.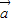 和
和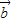 满足|
满足|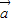 |=|
|=|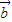 |=|
|=|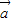 -
-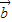 |,则
|,则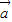 与
与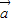 +
+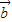 的夹角为60°.
的夹角为60°. ,
, ,
, .有下列命题:
.有下列命题: =(1,k),
=(1,k), =(-2,6),
=(-2,6), ∥b,则k=-3; ②若|
∥b,则k=-3; ②若| |=|
|=| |=|
|=| -
- |,则
|,则 与
与 +
+ 的夹角为60°;
的夹角为60°; +
+ |=|
|=| |+|
|+| |?
|? 与
与 的方向相同; ④|
的方向相同; ④| |+|
|+| |>|
|>| -
- |?
|? 与
与 的夹角为锐角;
的夹角为锐角; =(1,-3),
=(1,-3), =(-2,4),
=(-2,4), =(4,-6),则表示向量4
=(4,-6),则表示向量4 ,3
,3 -2
-2 ,
, 的有向线段首尾连接能构成三角形.
的有向线段首尾连接能构成三角形.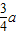
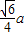
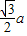
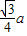
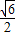 ;④AC垂直于截面BDE.
;④AC垂直于截面BDE.