题目内容
有下列命题:①在函数
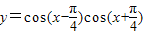 的图象中,相邻两个对称中心的距离为
的图象中,相邻两个对称中心的距离为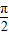 ;
;②若锐角α,β满足
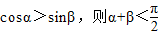 ;
;③函数f(x)=ax2-2ax-1有且仅有一个零点,则实数a=-1;
④要得到函数
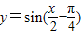 的图象,只需将
的图象,只需将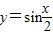 的图象向右平移
的图象向右平移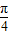 个单位.
个单位.⑤非零向量
 和
和 满足|
满足|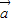 |=|
|=|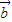 |=|
|=|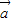 -
-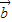 |,则
|,则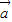 与
与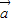 +
+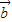 的夹角为60°.
的夹角为60°.其中所有真命题的序号是 .
【答案】分析:①将f(x)=cos(x+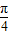 )化为f(x)=
)化为f(x)= cos2x,可求其周期,图象上相邻两个对称中心的距离是
cos2x,可求其周期,图象上相邻两个对称中心的距离是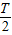 ,从而进行求解;
,从而进行求解;
②将sinβ=cos( -β),代入cosα>sinβ,进行求解;
-β),代入cosα>sinβ,进行求解;
③函数f(x)=)=ax2-2ax-1,利用图象的性质可得△=0,进行求解;
④函数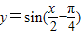 的图象,根据平移的性质,进行求解;
的图象,根据平移的性质,进行求解;
⑤非零向量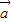 和
和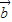 满足|
满足|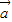 |=|
|=|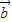 |=|
|=|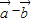 |,可以推出
|,可以推出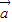 与
与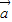 +
+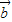 的夹角为30°,从而进行判断;
的夹角为30°,从而进行判断;
解答:解:①∵f(x)=cos(x-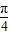 )cos(x+
)cos(x+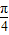 )=
)= cos2x,
cos2x,
∴其周期T=π,又图象上相邻两个对称中心的距离是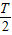 ,故①正确;
,故①正确;
②∵cosα>sinβ,cosα>cos(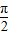 -β),可得cosα-cos(
-β),可得cosα-cos(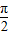 -β)>0,
-β)>0,
∵α,β是锐角,
∴α<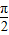 -β,即α+β<
-β,即α+β<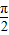 ;故②正确;
;故②正确;
③函数f(x)=ax2-2ax-1有且仅有一个零点,
∴△=(-2a)2-4a×(-1)=4a2+4a=0,解得a=-1,a=0(舍去),故③正确;
④要得到函数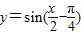 的图象,只需将函数y=sin
的图象,只需将函数y=sin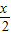 的图象向右平移
的图象向右平移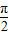 个单位可得,故④错误;
个单位可得,故④错误;
⑤非零向量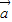 和
和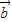 满足|
满足|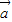 |=|
|=|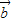 |=|
|=|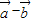 |,∴
|,∴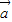 与
与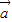 +
+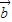 的夹角为30°,故⑤错误;
的夹角为30°,故⑤错误;
故答案为:①②③;
点评:此题考查三角函数的性质及函数的性质,考查的知识点比较全面,是一道基础题;
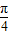 )化为f(x)=
)化为f(x)= cos2x,可求其周期,图象上相邻两个对称中心的距离是
cos2x,可求其周期,图象上相邻两个对称中心的距离是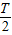 ,从而进行求解;
,从而进行求解;②将sinβ=cos(
 -β),代入cosα>sinβ,进行求解;
-β),代入cosα>sinβ,进行求解;③函数f(x)=)=ax2-2ax-1,利用图象的性质可得△=0,进行求解;
④函数
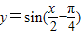 的图象,根据平移的性质,进行求解;
的图象,根据平移的性质,进行求解;⑤非零向量
 和
和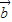 满足|
满足|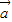 |=|
|=|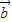 |=|
|=|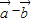 |,可以推出
|,可以推出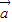 与
与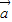 +
+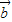 的夹角为30°,从而进行判断;
的夹角为30°,从而进行判断;解答:解:①∵f(x)=cos(x-
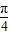 )cos(x+
)cos(x+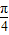 )=
)= cos2x,
cos2x,∴其周期T=π,又图象上相邻两个对称中心的距离是
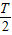 ,故①正确;
,故①正确;②∵cosα>sinβ,cosα>cos(
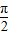 -β),可得cosα-cos(
-β),可得cosα-cos(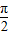 -β)>0,
-β)>0,∵α,β是锐角,
∴α<
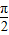 -β,即α+β<
-β,即α+β<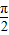 ;故②正确;
;故②正确;③函数f(x)=ax2-2ax-1有且仅有一个零点,
∴△=(-2a)2-4a×(-1)=4a2+4a=0,解得a=-1,a=0(舍去),故③正确;
④要得到函数
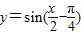 的图象,只需将函数y=sin
的图象,只需将函数y=sin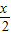 的图象向右平移
的图象向右平移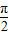 个单位可得,故④错误;
个单位可得,故④错误;⑤非零向量
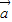 和
和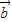 满足|
满足|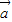 |=|
|=|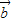 |=|
|=|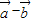 |,∴
|,∴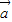 与
与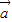 +
+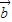 的夹角为30°,故⑤错误;
的夹角为30°,故⑤错误;故答案为:①②③;
点评:此题考查三角函数的性质及函数的性质,考查的知识点比较全面,是一道基础题;

练习册系列答案
相关题目
 有下列命题:
有下列命题: 的图象不过原点,则m=l或2;
的图象不过原点,则m=l或2; =(t,2),
=(t,2), =(-3,6),若向量
=(-3,6),若向量 与
与 的夹角为锐角,则实数t的取值范围是t<4;
的夹角为锐角,则实数t的取值范围是t<4;  的图象不过原点,则m=l或2;
的图象不过原点,则m=l或2; =(t,2),
=(t,2), =(-3,6),若向量
=(-3,6),若向量 与
与 的夹角为锐角,则实数t的取值范围是t<4;
的夹角为锐角,则实数t的取值范围是t<4;