题目内容
设命题p:不等式|2x-1|<x+a的解集是{x|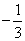 <x<3};命题q:不等式4x≥4ax2+1的解集是
<x<3};命题q:不等式4x≥4ax2+1的解集是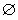 ,若“p或q”为真命题,试求实数a的值取值范围。
,若“p或q”为真命题,试求实数a的值取值范围。
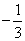 <x<3};命题q:不等式4x≥4ax2+1的解集是
<x<3};命题q:不等式4x≥4ax2+1的解集是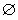 ,若“p或q”为真命题,试求实数a的值取值范围。
,若“p或q”为真命题,试求实数a的值取值范围。解:由|2x-1|<x+a,得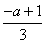 <x<a+1,
<x<a+1,
由题意,得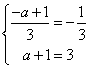 ,∴a=2,
,∴a=2,
∴命题p:a=2;
由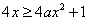 的解集是
的解集是 ,
,
得4ax2-4x+1≤0无解,
即对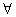 x∈R,4ax2-4x+1≤0恒成立,
x∈R,4ax2-4x+1≤0恒成立,
∴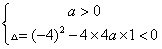 ,即a>1,
,即a>1,
∴命题q:a>1,
由“p或q”为真命题,得p、q中至少有一个真命题,
当p、q均为假命题,则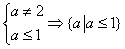 ,而
,而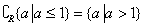 ,
,
∴实数a的值取值范围是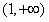 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目