题目内容
设命题P:复数z=(
)2-a(1-2i)+i对应的点在第二象限;
命题q:不等式|a-1|≥sinx对于x∈R恒成立;
如果“p且q”为假命题,“p或q”为真命题,求实数a的取值范围.
| 1-i | 1+i |
命题q:不等式|a-1|≥sinx对于x∈R恒成立;
如果“p且q”为假命题,“p或q”为真命题,求实数a的取值范围.
分析:把复数z化简成a+bi(a,b∈R)的形式,由其对应的点在第二象限,即实部小于0且虚部大于0求出a的范围;不等式
|a-1|≥sinx对于x∈R恒成立,即|a-1|≥1恒成立求出a的范围,最后根据“p且q”为假命题,“p或q”为真命题分类取交集求得实数a的取值范围.
|a-1|≥sinx对于x∈R恒成立,即|a-1|≥1恒成立求出a的范围,最后根据“p且q”为假命题,“p或q”为真命题分类取交集求得实数a的取值范围.
解答:解:由已知得:若命题P为真,
则复数z=(
)2-a(1-2i)+i=(
)2-a+2ai+i=-1-a+(2a+1)i对应的点在第二象限,
即:
,解得:a>-
;
由不等式|a-1|≥sinx对于x∈R恒成立,
则|a-1|≥1恒成立,
若命题q为真,则|a-1|≥1,即:a≥2或a≤0.
∵“p且q”为假命题,“p或q”为真命题
∴命题p真q假或命题p假q真
∴
,则:0<a<2;或
,则a≤-
.
∴所求实数a的取值范围为(-∞,-
]∪(0,2).
则复数z=(
| 1-i |
| 1+i |
| (1-i)2 |
| 2 |
即:
|
| 1 |
| 2 |
由不等式|a-1|≥sinx对于x∈R恒成立,
则|a-1|≥1恒成立,
若命题q为真,则|a-1|≥1,即:a≥2或a≤0.
∵“p且q”为假命题,“p或q”为真命题
∴命题p真q假或命题p假q真
∴
|
|
| 1 |
| 2 |
∴所求实数a的取值范围为(-∞,-
| 1 |
| 2 |
点评:本题考查了复数代数形式的乘除运算,复数的除法,采用分子分母同时乘以分母的共轭复数,考查了复合命题的真假判断,命题p与命题q中只要有一个为假命题,则“p且q”为假命题,只要有一个为真命题,则“p或q”为真命题,此题是中档题.

练习册系列答案
相关题目
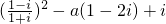 对应的点在第二象限;
对应的点在第二象限;