题目内容
．（本小题满分12分）如图所示，矩形ABCD的边AB=
，BC=2，PA⊥平面ABCD，PA=2，现有数据：
①
；②
；③
；建立适当的空间直角坐标系，
（I）当BC边上存在点Q，使PQ⊥QD时，可能取所给数据中的哪些值?请说明理由；
（II）在满足（I）的条件下，若取所给数据的最小值时，这样的点Q有几个? 若沿BC方向依次记为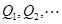
，试求二面角
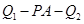的大小.
【答案】
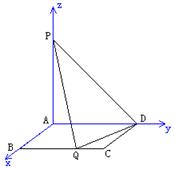
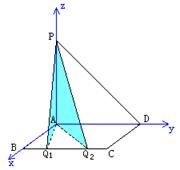
解：（I）建立如图所示的空间直角坐标系,则各点坐标分别为:
，
，
，
，
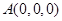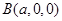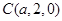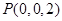
设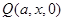
(0≤x≤2)， …………………2分
∵
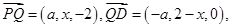∴由PQ⊥QD得
。
∵
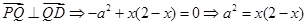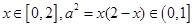……………4分
∴在所给数据中，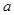
可取
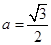和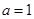
两个值. ……6分
(II) 由(Ⅰ)知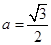，此时
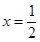或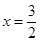
，即满足条件的点Q有两个，…8分
根据题意，其坐标为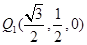
和
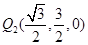，……9分
∵PA⊥平面ABCD，∴PA⊥AQ1，PA⊥AQ2，
∴∠Q1AQ2就是二面角Q1-PA-Q2的平面角.……………………10分
由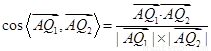
=
，
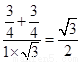得∠Q1AQ2=30°，∴二面角Q1-PA-Q2的大小为30°.………………………12分
【解析】略
练习册系列答案
相关题目
，且
。①求
的最大值及最小值；②求
、
、
.现有3名工人独立地从中任选一个项目参与建设.求：
