题目内容
(本题满分12分)
某班一信息奥赛同学编了下列运算程序,将数据输入满足如下性质:
①输入1时,输出结果是 ;
;
②输入整数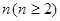 时,输出结果
时,输出结果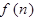 是将前一结果
是将前一结果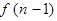 先乘以3n-5,再除以3n+1.
先乘以3n-5,再除以3n+1.
(1) 求f(2),f(3),f(4);
(2) 试由(1)推测f(n)(其中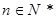 )的表达式,并给出证明.
)的表达式,并给出证明.
某班一信息奥赛同学编了下列运算程序,将数据输入满足如下性质:
①输入1时,输出结果是
 ;
;②输入整数
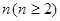 时,输出结果
时,输出结果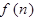 是将前一结果
是将前一结果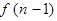 先乘以3n-5,再除以3n+1.
先乘以3n-5,再除以3n+1.(1) 求f(2),f(3),f(4);
(2) 试由(1)推测f(n)(其中
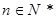 )的表达式,并给出证明.
)的表达式,并给出证明.(1)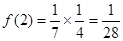 ;
;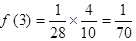 ;
;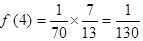 .
.
(2)猜想: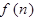
 (其中
(其中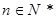 ),以下用数学归纳法证明:见解析。
),以下用数学归纳法证明:见解析。
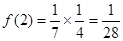 ;
;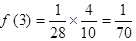 ;
;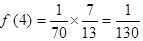 .
. (2)猜想:
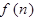
 (其中
(其中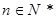 ),以下用数学归纳法证明:见解析。
),以下用数学归纳法证明:见解析。本试题主要是考查了数列的归纳猜想思想的运用,以及运用数学归纳法求证恒等式的综合运用。
(1)由题设条件知f(1)= ,
,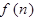 =
=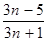
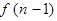 ,对于n令值,然后得到前几个值。
,对于n令值,然后得到前几个值。
(2)猜想: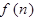
 (其中
(其中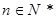 )并运用数学归纳法,运用两步来证明其成立。
)并运用数学归纳法,运用两步来证明其成立。
解:由题设条件知f(1)= ,
,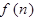 =
=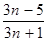
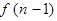 ,
,
 ;
;
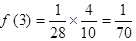 ;
;
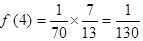 . ………………………………3分
. ………………………………3分
(2)猜想: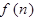
 (其中
(其中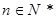 )……………………5分
)……………………5分
以下用数学归纳法证明:
(1) 当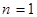 时,
时,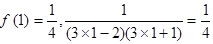 ,
,
所以此时猜想成立。 ………………………………6分
(2) 假设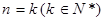 时,
时,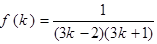 成立
成立
那么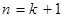 时,
时,
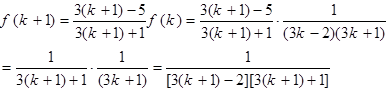 ……………9分
……………9分
所以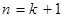 时,猜想成立。
时,猜想成立。
由(1)(2)知,猜想: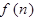
 (其中
(其中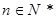 )成立。
)成立。
…………………………12分
(1)由题设条件知f(1)=
 ,
,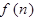 =
=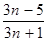
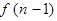 ,对于n令值,然后得到前几个值。
,对于n令值,然后得到前几个值。(2)猜想:
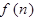
 (其中
(其中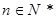 )并运用数学归纳法,运用两步来证明其成立。
)并运用数学归纳法,运用两步来证明其成立。解:由题设条件知f(1)=
 ,
,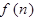 =
=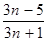
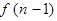 ,
, ;
;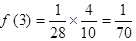 ;
;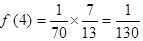 . ………………………………3分
. ………………………………3分(2)猜想:
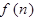
 (其中
(其中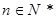 )……………………5分
)……………………5分以下用数学归纳法证明:
(1) 当
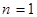 时,
时,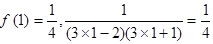 ,
,所以此时猜想成立。 ………………………………6分
(2) 假设
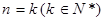 时,
时,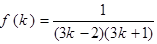 成立
成立那么
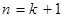 时,
时,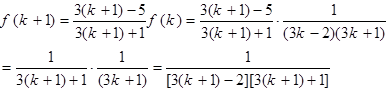 ……………9分
……………9分所以
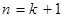 时,猜想成立。
时,猜想成立。由(1)(2)知,猜想:
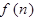
 (其中
(其中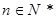 )成立。
)成立。…………………………12分

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
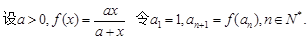
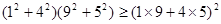 ;
;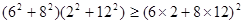 ;
;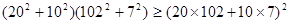 .
. +
+ +…+
+…+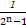 <n(n∈N*,n>1)时,第一步应验证的不等式是 .
<n(n∈N*,n>1)时,第一步应验证的不等式是 .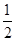 +
+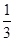 +…+
+…+ <n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )
<n(n∈N*,n>1)时,在证明过程的第二步从n=k到n=k+1时,左边增加的项数是 ( )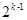
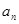 }的前n项和为
}的前n项和为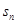 ,
,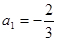 ,满足
,满足 ,计算
,计算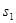 ,
,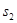 ,
,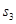 ,
,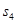 ,并猜想
,并猜想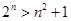 对于
对于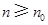 的自然数
的自然数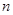 都成立”时,第一步证明中的起始值
都成立”时,第一步证明中的起始值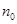 应取_____________.
应取_____________.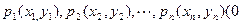 <
<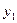 <
<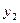 <…<
<…<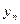 )是曲线C
)是曲线C
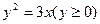 上的n个点,点
上的n个点,点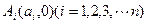 在x轴的正半轴上,且⊿
在x轴的正半轴上,且⊿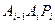 是正三角形(
是正三角形(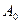 是坐标原点)。
是坐标原点)。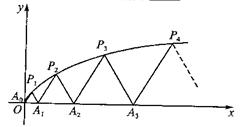
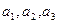
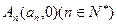 的横坐标
的横坐标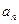 关于n的表达式并用数学归纳法证明
关于n的表达式并用数学归纳法证明