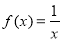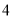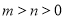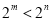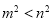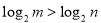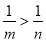题目内容
已知 ,函数
,函数 .
.
(I)证明:函数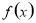 在
在 上单调递增;
上单调递增;
(Ⅱ)求函数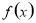 的零点.
的零点.
(I)详见解析;(Ⅱ)详见解析;
【解析】
试题分析:(I)先在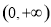 上任取两变量
上任取两变量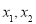 ,设
,设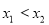 ,再对
,再对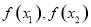 作差变形化简,判断
作差变形化简,判断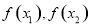 大小确定单调性.
大小确定单调性.
(Ⅱ)要求函数f(x)的零点,即求方程f(x)=0的根,对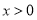 和
和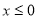 分情况求解,其中当
分情况求解,其中当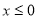 时,令
时,令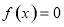 , 即
, 即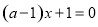 ,对此方程中参数a对根的情况进行讨论求解.
,对此方程中参数a对根的情况进行讨论求解.
试题解析: (1)证明:在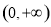 上任取两个实数
上任取两个实数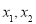 ,且
,且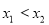 ,
,
则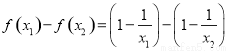

 . 2分
. 2分
∵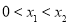 , ∴
, ∴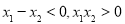 .
.
∴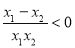 , 即
, 即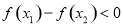 . ∴
. ∴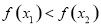 .
.
∴函数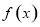 在
在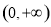 上单调递增. 4分[K]
上单调递增. 4分[K]
(2) (ⅰ)当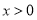 时, 令
时, 令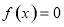 , 即
, 即 , 解得
, 解得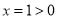 .
.
∴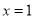 是函数
是函数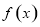 的一个零点. 6分
的一个零点. 6分
(ⅱ)当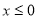 时, 令
时, 令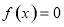 , 即
, 即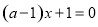 .(※)
.(※)
①当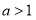 时, 由(※)得
时, 由(※)得 ,∴
,∴ 是函数
是函数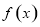 的一个零点; 8分
的一个零点; 8分
②当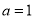 时, 方程(※)无解;
时, 方程(※)无解;
③当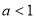 时, 由(※)得
时, 由(※)得 ,(不合题意,舍去) 10分
,(不合题意,舍去) 10分
综上, 当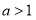 时, 函数
时, 函数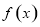 的零点是
的零点是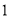 和
和 ;
;
当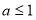 时, 函数
时, 函数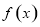 的零点是
的零点是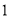 . 12分
. 12分
考点:1.函数单调性的判断与证明;2.分段函数的解析式求法及其图象的作法;3.函数的零点.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目