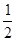题目内容
已知两不共线向量 =(cosα,sinα),
=(cosα,sinα), =(cosβ,sinβ),则下列说法不正确的是
=(cosβ,sinβ),则下列说法不正确的是
- A.|
 |=|
|=| |=1
|=1 - B.(
 +
+ )⊥(
)⊥( -
- )
) - C.
 与
与 的夹角等于α-β
的夹角等于α-β - D.
 与
与 在
在 +
+ 方向上的投影相等
方向上的投影相等
C
分析:由模长公式可得 =
= =1,故A正确;由数量积为0可得向量垂直,故B正确;由夹角公式可得向量夹角的余弦值,但角的范围不一定,故C错误;而D由投影相等可与模长相等等价,结合A可知正确,故可得答案.
=1,故A正确;由数量积为0可得向量垂直,故B正确;由夹角公式可得向量夹角的余弦值,但角的范围不一定,故C错误;而D由投影相等可与模长相等等价,结合A可知正确,故可得答案.
解答:由模长公式可得 =
=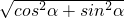 =1,
=1, =
=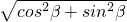 =1,即
=1,即 =
= ,故A正确;
,故A正确;
∵( )•(
)•( )=|
)=| |2-|
|2-| |2=0,∴(
|2=0,∴( )⊥(
)⊥( ),故B正确;
),故B正确;
由夹角公式可得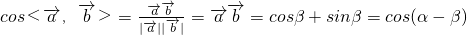 .
.
当α-β∈[0,π]时,< >=α-β;当α-β∉[0,π]时,<
>=α-β;当α-β∉[0,π]时,< >≠α-β,故C不正确;
>≠α-β,故C不正确;
由投影相等可得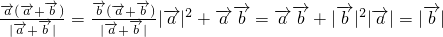 ,故D正确.
,故D正确.
故选C
点评:本题考查向量的数量积的运算,涉及向量的模长和投影及夹角,属中档题.
分析:由模长公式可得
 =
= =1,故A正确;由数量积为0可得向量垂直,故B正确;由夹角公式可得向量夹角的余弦值,但角的范围不一定,故C错误;而D由投影相等可与模长相等等价,结合A可知正确,故可得答案.
=1,故A正确;由数量积为0可得向量垂直,故B正确;由夹角公式可得向量夹角的余弦值,但角的范围不一定,故C错误;而D由投影相等可与模长相等等价,结合A可知正确,故可得答案.解答:由模长公式可得
 =
=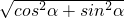 =1,
=1, =
=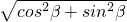 =1,即
=1,即 =
= ,故A正确;
,故A正确;∵(
 )•(
)•( )=|
)=| |2-|
|2-| |2=0,∴(
|2=0,∴( )⊥(
)⊥( ),故B正确;
),故B正确;由夹角公式可得
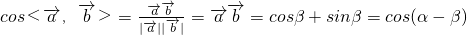 .
.当α-β∈[0,π]时,<
 >=α-β;当α-β∉[0,π]时,<
>=α-β;当α-β∉[0,π]时,< >≠α-β,故C不正确;
>≠α-β,故C不正确;由投影相等可得
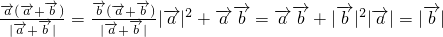 ,故D正确.
,故D正确.故选C
点评:本题考查向量的数量积的运算,涉及向量的模长和投影及夹角,属中档题.

练习册系列答案
相关题目
已知两不共线向量a=(cosα,sinα),b=(cosβ,sinβ),则下列说法不正确的是( )
| A、(a+b)⊥(a-b) | B、a与b的夹角等于α-β | C、|a+b|+|a-b|>2 | D、a与b在a+b方向上的投影相等 |
 ,
, ,则下列说法不正确的是(
)
,则下列说法不正确的是(
) B.
B.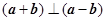
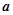 与
与 的夹角等于
的夹角等于 D.
D. 方向上的投影相等
方向上的投影相等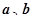 ,若
,若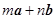 与
与 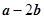 共线,则
共线,则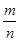 等于 ( )
等于 ( )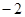 ; B.
; B.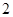 C.
C.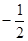 D.
D.