题目内容
定义在R上的函数 满足f(1)=1,且对任意x∈R都有
满足f(1)=1,且对任意x∈R都有 ,则不等式
,则不等式 的解集为 ( )
的解集为 ( )
| A.(1,2) | B.(0,1) | C.(1,+∞) | D.(-1,1) |
D
解析试题分析:记 ,则
,则 是偶函数,当
是偶函数,当 时,
时, =
=
 ,∵
,∵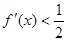 ,∴
,∴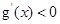 ,故当
,故当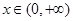 时,
时, 递减,又
递减,又 是偶函数,故当
是偶函数,故当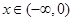 时
时 递增,且
递增,且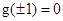 ,所以解集为(-1,1).
,所以解集为(-1,1).
考点:1、复合函数的导数;2、函数的奇偶性;3、导数在单调性上的应用.

练习册系列答案
相关题目
函数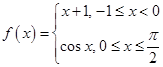 的图象与
的图象与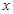 轴所围成的封闭图形的面积为( )
轴所围成的封闭图形的面积为( )
A.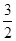 | B.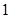 | C. | D. |
已知函数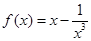 ,则
,则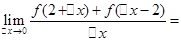 ( )
( )
A.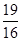 | B.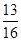 | C.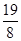 | D.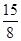 |
已知不等式 的解集
的解集 ,则函数
,则函数 单调递增区间为( )
单调递增区间为( )
A.(- | B.(-1,3) | C.( -3,1) | D.( |
函数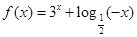 的零点所在区间为( )
的零点所在区间为( )
A.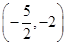 | B.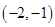  | C.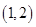 | D.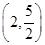 |
已知函数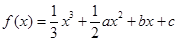 在
在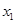 处取得极大值,在
处取得极大值,在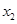 处取得最小值,满足
处取得最小值,满足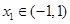 ,
,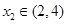 ,则
,则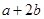 的取值范围是( )
的取值范围是( )
A.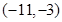 | B.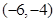 | C.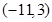 | D. |
已知函数f(x)的定义域为R,对任意 ,有
,有 ,且
,且 ,则f(x)<3x+6的解集为( )
,则f(x)<3x+6的解集为( )
| A.(-1, 1) | B.(-1,+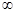 ) ) | C.(-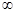 ,-1) ,-1) | D.(-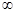 ,+ ,+ ) ) |
已知函数f(x)(x∈R)满足 >f(x),则 ( )
>f(x),则 ( )
A.f(2)< f(0) f(0) | B.f(2)≤ f(0) f(0) |
C.f(2)= f(0) f(0) | D.f(2)> f(0) f(0) |
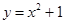 在点
在点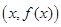 处的切线的斜率为
处的切线的斜率为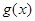 ,则函数
,则函数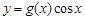 的部分图象可以为( )
的部分图象可以为( )