Question

【题目】将一个半径为3分米，圆心角为α（α∈（0，2π））的扇形铁皮焊接成一个容积为V立方分米的圆锥形无盖容器（忽略损耗）．
（1）求V关于α的函数关系式；
（2）当α为何值时，V取得最大值；
（3）容积最大的圆锥形容器能否完全盖住桌面上一个半径为0.5分米的球？请说明理由．

Answer 1

【答案】
（1）解：由题意知圆锥的母线l=3，设圆锥的底面半径为r，则2πr=3α，

∴r= ，∴圆锥的高h= = = ．

∴V= =

（2）解：V= = ≤ =2 ．

当且仅当4π2﹣α2= 即α= 时，取等号．

∴当α= 时，体积V取得最大值

（3）解：当圆锥体积最大时，圆锥的底面半径r= ．

设圆锥轴截面△ABC的内切圆⊙O半径为R，如图所示，

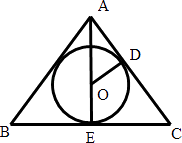
则OD=R，CD=CE= ，AC=3，∴AE= ，AD=3﹣ ．

由△AOD∽△ACE得 ，

∴ ，解得R=3 ≈0.8．

∵0.8＞0.5，

∴容积最大的圆锥形容器能完全盖住桌面上一个半径为0.5分米的球．

【解析】（1）根据面积得出圆锥的底面半径，利用勾股定理求出圆锥的高，代入体积公式即可；（2）利用基本不等式得出体积的最值及取得最值得条件；（3）求出圆锥内切球的半径，与0.5比较大小．
【考点精析】掌握基本不等式在最值问题中的应用和旋转体（圆柱、圆锥、圆台）是解答本题的根本，需要知道用基本不等式求最值时（积定和最小，和定积最大），要注意满足三个条件“一正、二定、三相等”；常见的旋转体有：圆柱、圆锥、圆台、球．