题目内容
选考题：请考生在第22、23、24题中任选一题做答，如果多做，则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目对应的题号涂黑。本题满分10分．
22．选修4－1：几何证明选讲
如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于点D，DE⊥AC，
交AC的延长线于点E.OE交AD于点F.
（1）求证：DE是⊙O的切线；
（2）若
，求
的值.
22．选修4－1：几何证明选讲
如图，AB是⊙O的直径，AC是弦，∠BAC的平分线AD交⊙O于点D，DE⊥AC，
交AC的延长线于点E.OE交AD于点F.
（1）求证：DE是⊙O的切线；
（2）若
，求的值.
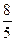
略证（１）连结OD，可得∠ODA=∠OAD=∠DAC ……2分
∴OD∥AE 又AE⊥DE …………3分
∴DE⊥OD，又OD为半径 ∴ DE是的⊙O切线 …………5分
⑵ 提示：过D作DH⊥AB于H 则有∠DOH=∠CAB
Cos∠DOH=cos∠CAB=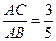
……………………6分
设OD=5x，则AB=10x，OH=3x，DH=4x
∴AH="8x " AD2=80x2
由△AED∽△ADB可得 AD2="AE·AB=AE·10x " ∴AE=8X…………8分
又由△AEF∽△DOF 可得AF∶DF= AE∶OD =；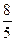
∴
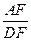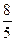=……10分
∴OD∥AE 又AE⊥DE …………3分
∴DE⊥OD，又OD为半径 ∴ DE是的⊙O切线 …………5分
⑵ 提示：过D作DH⊥AB于H 则有∠DOH=∠CAB
Cos∠DOH=cos∠CAB=
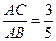……………………6分设OD=5x，则AB=10x，OH=3x，DH=4x
∴AH="8x " AD2=80x2由△AED∽△ADB可得 AD2="AE·AB=AE·10x " ∴AE=8X…………8分
又由△AEF∽△DOF 可得AF∶DF= AE∶OD =
；∴
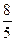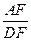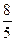=……10分
练习册系列答案
阅读快车系列答案
相关题目
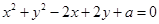表示圆，则实数
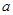的取值范围是（ ）
和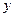
轴相切，圆心在直线
上，且被直线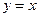
截得的弦长为
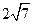，求圆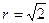
，BC=1，求AD。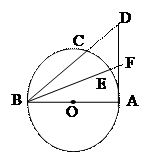
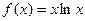的图象在
处的切线为
, 则
上的点的最近距离是 （ ）
与
是
的直径，
是
交
，连
交
，若
，则
．
+(y+1)
，则圆心
及半径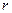
分别为 （ ）
、圆心
，半径
； 
、圆心
； 
、圆心
，半径
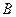、圆心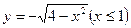
的长度是 .