题目内容
【题目】已知函数![]()
![]() .
.
(Ⅰ) 求函数![]() 的单调区间;
的单调区间;
(Ⅱ) 当![]() 时,求函数
时,求函数![]() 在
在![]() 上最小值.
上最小值.
【答案】(Ⅰ)见解析;(Ⅱ)当![]() 时,函数
时,函数![]() 的最小值是
的最小值是![]() ;当
;当![]() 时,函数
时,函数![]() 的最小值是
的最小值是![]()
【解析】
(1)求出导函数,并且解出它的零点x=,再分区间讨论导数的正负,即可得到函数f(x)的单调区间;
(2)分三种情况加以讨论,结合函数的单调性与函数值的大小比较,即可得到当0<a<ln 2时,函数f(x)的最小值是-a;当a≥ln2时,函数f(x)的最小值是ln2-2a.
![]() 函数
函数![]() 的定义域为
的定义域为![]() .
.![]()
因为![]() ,令
,令![]() ,可得
,可得![]() ;
;
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
综上所述:可知函数![]() 的单调递增区间为
的单调递增区间为![]() ,单调递减区间为
,单调递减区间为![]()
![]() 当
当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是减函数,
上是减函数,![]() 的最小值是
的最小值是![]()
![]() 当
当![]() ,即
,即![]() 时,函数
时,函数![]() 在区间
在区间![]() 上是增函数,
上是增函数,
![]() 的最小值是
的最小值是![]()
![]() 当
当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
又![]() ,
,![]() 当
当![]() 时,
时,![]() 的最小值是
的最小值是![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]()
综上所述,结论为当![]() 时,函数
时,函数![]() 的最小值是
的最小值是![]() ;
;
当![]() 时,函数
时,函数![]() 的最小值是
的最小值是![]() .
.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案【题目】十三届全国人大二次会议于2019年3月5日在京召开.为了了解某校大学生对两会的关注程度,学校媒体在开幕后的第二天,从学生中随机抽取了180人,对是否收看2019年两会开幕会情况进行了问卷调查,统计数据得到列联表如下:
收看 | 没收看 | 合计 | |
男生 | 40 | ||
女生 | 30 | 60 | |
合计 |
(1)请完成列联表;
(2)根据上表说明,能否有99%的把握认为该校大学生收看开幕会与性别有关?(结果精确到0.001)
附: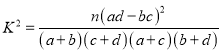 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
【题目】某公司近年来科研费用支出![]() 万元与公司所获得利润
万元与公司所获得利润![]() 万元之间有如下的统计数据:
万元之间有如下的统计数据:
x | 2 | 3 | 4 | 5 |
Y | 18 | 27 | 32 | 35 |
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)试根据(1)求出的线性回归方程,预测该公司科研费用支出为10万元时公司所获得的利润.
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
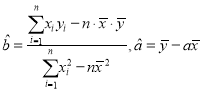
参考数据:2×18+3×27+4×32+5×35=420
