题目内容
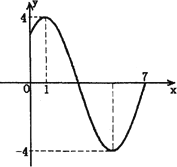
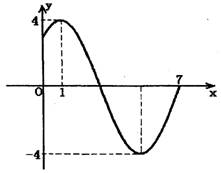
如图,已知函数f(x)=Asin(ωx+φ)(A>0,|φ|< )图像上一个最高点坐标为(2,2
)图像上一个最高点坐标为(2,2 ),这个最高点到相邻最低点的图像与x轴交于点(5,0).
),这个最高点到相邻最低点的图像与x轴交于点(5,0).

(1)求f(x)的解析式;
(2)是否存在正整数m,使得将函数f(x)的图像向右平移m个单位后得到一个偶函数的图像?若存在,求m的最小值;若不存在,请说明理由.
【答案】
(1)f(x)=2 sin
sin ,
,
(2)m的最小值为4.
【解析】
试题分析:解:(1)由题意知A=2 ,
,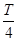 =3,
=3,
∴T=12,∴ω=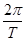 =
=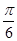 ,
,
∴f(x)=2 sin
sin ,
,
∵图像过(2,2 ),∴2
),∴2 =2
=2 sin
sin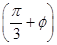 ,
,
∴sin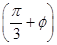 =1,
=1,
令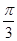 +φ=
+φ=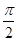 ,∴φ=
,∴φ=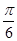 ,
,
∴f(x)=2 sin
sin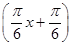 . 6分
. 6分
(2)假设存在m,则有
f(x-m)=2 sin
sin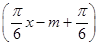
=2 cos
cos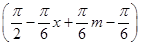
=2 cos
cos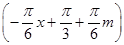
∵f(x-m)为偶函数,
∴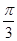 +
+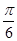 m=kπ,k∈Z
m=kπ,k∈Z
∴m=6k-2,∴k=1时m=4.
∴存在m,m的最小值为4. 13分
考点:三角函数的图象与解析式
点评:主要是考查了三角函数的解析式以及性质的运用,属于中档题。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目