题目内容
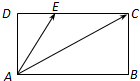 在矩形ABCD中,
在矩形ABCD中,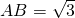 ,BC=1,E是CD上一点,且
,BC=1,E是CD上一点,且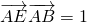 ,则
,则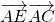 的值为
的值为
- A.3
- B.2
- C.

- D.

B
分析:设 =
=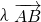 ,可得
,可得 =
=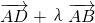 ,代入
,代入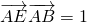 算出
算出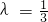 ,从而得到
,从而得到 关于
关于 、
、 表示式,再由
表示式,再由 =
=
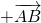 ,代入
,代入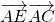 结合题中数据即可算出
结合题中数据即可算出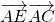 的值.
的值.
解答:设 =
=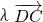 ,即
,即 =
=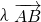
∵ =
=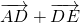 =
=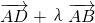
∴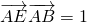 即(
即(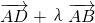 )
) =1
=1
∵AD、AB互相垂直,可得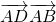 =0
=0
∴(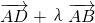 )
) =λ
=λ =3λ=1,解之得
=3λ=1,解之得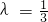
由此可得 =
=
 ,
, =
=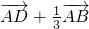
∵ =
=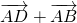
∴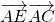 =(
=(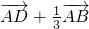 )(
)(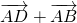 )=
)=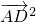 +
+
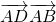 +
+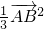 =12+
=12+ ×
×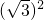 =2
=2
故选:B
点评:本题在矩形中,已知边AB、AD的长度和点E分DC的比值,求向量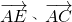 的数量积.着重考查了平面向量数量积的定义及运算性质等知识,属于基础题.
的数量积.着重考查了平面向量数量积的定义及运算性质等知识,属于基础题.
分析:设
 =
=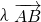 ,可得
,可得 =
=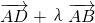 ,代入
,代入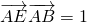 算出
算出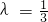 ,从而得到
,从而得到 关于
关于 、
、 表示式,再由
表示式,再由 =
=
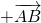 ,代入
,代入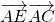 结合题中数据即可算出
结合题中数据即可算出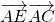 的值.
的值.解答:设
 =
=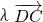 ,即
,即 =
=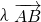
∵
 =
=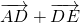 =
=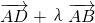
∴
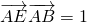 即(
即(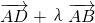 )
) =1
=1∵AD、AB互相垂直,可得
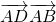 =0
=0∴(
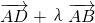 )
) =λ
=λ =3λ=1,解之得
=3λ=1,解之得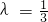
由此可得
 =
=
 ,
, =
=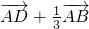
∵
 =
=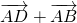
∴
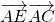 =(
=(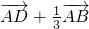 )(
)(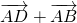 )=
)=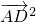 +
+
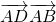 +
+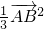 =12+
=12+ ×
×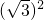 =2
=2故选:B
点评:本题在矩形中,已知边AB、AD的长度和点E分DC的比值,求向量
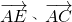 的数量积.着重考查了平面向量数量积的定义及运算性质等知识,属于基础题.
的数量积.着重考查了平面向量数量积的定义及运算性质等知识,属于基础题. 
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
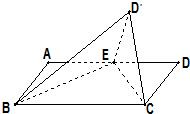 如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.
如图所示,在矩形ABCD中,AD=2AB=2,点E是AD的中点,将△DEC沿CE折起到△D′EC的位置,使二面角D′-EC-B是直二面角.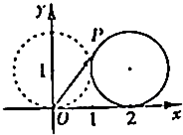 (1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,
(1)如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,