题目内容
(2013•潍坊一模)已知抛物线y2=2px(p>0)的焦点F与双曲
-
=1的右焦点重合,抛物线的准线与x轴的交点为K,点A在抛物线上且|AK|=
|AF|,则A点的横坐标为( )
| x2 |
| 4 |
| y2 |
| 5 |
| 2 |
分析:根据双曲线
-
=1得出其右焦点坐标,可知抛物线的焦点坐标,从而得到抛物线的方程和准线方程,进而可求得K的坐标,设A(x0,y0),过A点向准线作垂线AB,则B(-3,y0),根据|AK|=
|AF|及AF=AB=x0-(-3)=x0+3,进而可求得A点坐标.
| x2 |
| 4 |
| y2 |
| 5 |
| 2 |
解答: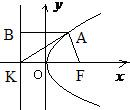 解:∵双曲线
解:∵双曲线
-
=1,其右焦点坐标为(3,0).
∴抛物线C:y2=12x,准线为x=-3,
∴K(-3,0)
设A(x0,y0),过A点向准线作垂线AB,则B(-3,y0)
∵|AK|=
|AF|,又AF=AB=x0-(-3)=x0+3,
∴由BK2=AK2-AB2得BK2=AB2,从而y02=(x0+3)2,即12x0=(x0+3)2,
解得x0=3.
故选B.
 解:∵双曲线
解:∵双曲线| x2 |
| 4 |
| y2 |
| 5 |
∴抛物线C:y2=12x,准线为x=-3,
∴K(-3,0)
设A(x0,y0),过A点向准线作垂线AB,则B(-3,y0)
∵|AK|=
| 2 |
∴由BK2=AK2-AB2得BK2=AB2,从而y02=(x0+3)2,即12x0=(x0+3)2,
解得x0=3.
故选B.
点评:本题主要考查了抛物线的简单性质.考查了学生对抛物线基础知识的熟练掌握.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•潍坊一模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为BC中点,则
(2013•潍坊一模)如图,在边长为2的菱形ABCD中,∠BAD=60°,E为BC中点,则 (2013•潍坊一模)已知数列{an}的各项排成如图所示的三角形数阵,数阵中每一行的第一个数a1,a2,a4,a7,…构成等差数列{bn},Sn是{bn}的前n项和,且b1=a1=1,S5=15.
(2013•潍坊一模)已知数列{an}的各项排成如图所示的三角形数阵,数阵中每一行的第一个数a1,a2,a4,a7,…构成等差数列{bn},Sn是{bn}的前n项和,且b1=a1=1,S5=15.