题目内容
一动圆经过点Q(0,
)且和直线2y+1=0相切,记其圆心的轨迹为曲线C.
(1)求曲线C的方程.
(2)是否存在正数t,对于过点T(0,t)且与曲线C有两个交点R,S的任一直线,都有
•
<0,若存在,求出t的取值范围;若不存在,请说明理由:
| 1 |
| 2 |
(1)求曲线C的方程.
(2)是否存在正数t,对于过点T(0,t)且与曲线C有两个交点R,S的任一直线,都有
| QR |
| QS |
分析:(1)设出圆心的坐标C(x,y),根据半径的关系,动圆经过点Q(0,
)且和直线2y+1=0相切,C点与Q点的距离等于圆半径的平方,而y-
也等于半径的平方,故求出C的轨迹方程;
(2)设出点R(x1,y1),S(x2,y2)设出直线y=kx+t,与曲线C的方程进行联立,求出x1+x2,和x1•x2,根据向量的内积公式写出
表达式,让其小于0,求出t的范围;
| 1 |
| 2 |
| 1 |
| 2 |
(2)设出点R(x1,y1),S(x2,y2)设出直线y=kx+t,与曲线C的方程进行联立,求出x1+x2,和x1•x2,根据向量的内积公式写出
| QR |
| •QS |
解答:解:(1)设圆心C(x,y),半径为r,
∵动圆经过点Q(0,
),∴(x-0)2+(y-
)2=r2;
∵圆和直线2y+1=0相切,
∴y+
=r,
∴(x-0)2+(y-
)2=(y+
)2,
∴曲线C的方程为:x2=2y;
(2)∵直线过点T(0,t)且与曲线C有两个交点R,S,
∴可设y=kx+t,点R(x1,y1),S(x2,y2),点Q(0,
)
∴
=x1x2+y1y2-
(y1+y2),
联立方程:
消去y得,
x2-2kx-2t=0,△=(-2k)2-4×(-2t)=4k2+8t>0,
∴k2>-2t,-k2<2t,
∴x1+x2=2k,x1•x2=-2t;
∴y1+y2=(kx1+t)+(kx2+t)=2k2+2t,
y1y2=(kx1+t)•(kx2+t)=k2x1•x2+t2+kt(x1+x2)=t2,
∴
=x1x2+y1y2-
(y1+y2)=-2t+t2-
×(2k2+2t2)=t2-3t-k2-t-
<t2-3t+2t-
=t2-t-
=(t-1)2-
<0,
∴1-
<t<1+
,满足t>0,
∴t的取值范围:1-
<t<1+
;
∵动圆经过点Q(0,
| 1 |
| 2 |
| 1 |
| 2 |
∵圆和直线2y+1=0相切,
∴y+
| 1 |
| 2 |
∴(x-0)2+(y-
| 1 |
| 2 |
| 1 |
| 2 |
∴曲线C的方程为:x2=2y;
(2)∵直线过点T(0,t)且与曲线C有两个交点R,S,
∴可设y=kx+t,点R(x1,y1),S(x2,y2),点Q(0,
| 1 |
| 2 |
∴
| QR |
| •QS |
| 1 |
| 2 |
联立方程:
|
x2-2kx-2t=0,△=(-2k)2-4×(-2t)=4k2+8t>0,
∴k2>-2t,-k2<2t,
∴x1+x2=2k,x1•x2=-2t;
∴y1+y2=(kx1+t)+(kx2+t)=2k2+2t,
y1y2=(kx1+t)•(kx2+t)=k2x1•x2+t2+kt(x1+x2)=t2,
∴
| QR |
| •QS |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
∴1-
| ||
| 2 |
| ||
| 2 |
∴t的取值范围:1-
| ||
| 2 |
| ||
| 2 |
点评:第一问考查轨迹方程,正好是抛物线,第二问是关于存在性问题,一般假设存在,然后进行求解,本题是关于圆锥曲线的问题,是高考的热点问题,难度中等偏上;

练习册系列答案
相关题目
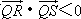 ?,若存在,求出t的取值范围;若不存在,请说明理由:
?,若存在,求出t的取值范围;若不存在,请说明理由: 为该平面上一动点,作
为该平面上一动点,作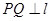 ,垂足为Q,且(
,垂足为Q,且(
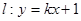 与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由
与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由 )且和直线2y+1=0相切,记其圆心的轨迹为曲线C.
)且和直线2y+1=0相切,记其圆心的轨迹为曲线C.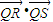 <0,若存在,求出t的取值范围;若不存在,请说明理由:
<0,若存在,求出t的取值范围;若不存在,请说明理由: