题目内容
(本题满分12分)已知平面上一定点C(4,0)和一定直线 为该平面上一动点,作
为该平面上一动点,作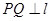 ,垂足为Q,且(
,垂足为Q,且(
(Ⅰ)问点P在什么曲线上?并求出该曲线的方程;
(Ⅱ)设直线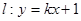 与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由
与(1)中的曲线交于不同的两点A、B,是否存在实数k,使 得以线段AB为直径的圆经过点D(0,-2)?若存在,求出k的值,若不存在,说明理由
【答案】
解:(Ⅰ)设P的坐标为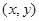 ,由
,由 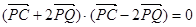 得
得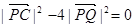
∴(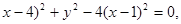 化简得
化简得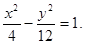
∴P点在双曲线上,其方程为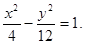
(Ⅱ)设A、B点的坐标分别为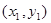 、
、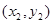 ,由
,由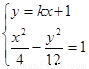 得
得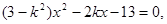
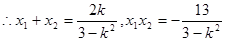 , ∵AB与双曲线交于两点,∴△>0,
, ∵AB与双曲线交于两点,∴△>0,
即 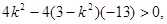 解得
解得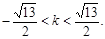
∵若以AB为直径的圆过D(0,-2),则AD⊥BD, ∴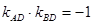 ,即
,即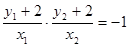
∴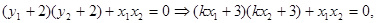 ∴
∴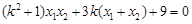
∴ ,
, 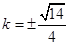
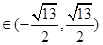
即存在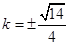 符合要求.
符合要求.
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的三个内角
的三个内角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 .
. ,且
,且 .(1)求
.(1)求 .求
.求 .
. ,
, 的等比中项。
的等比中项。 是等差数列;(2)若
是等差数列;(2)若 的前n项和为Tn,求Tn。
的前n项和为Tn,求Tn。 :
: 的长轴长是短轴长的
的长轴长是短轴长的 倍,
倍, ,
, 是它的左,右焦点.
是它的左,右焦点. ,且
,且 ,
, ,求
,求 作以
作以 (
( 是切点),且使
是切点),且使 ,求动点
,求动点 的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量
的长轴,短轴端点分别是A,B,从椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点,向量 与
与 是共线向量
是共线向量 分别是左右焦点,求
分别是左右焦点,求 的取值范围
的取值范围