Question

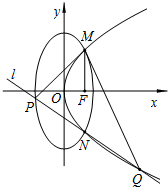（2013•永州一模）在直角坐标系xoy中，椭圆C₁：

y2

a2

+

x2

b2

=1(a＞b＞0)的离心率e=

3

2

，F是抛物线C₂：y²=4x的焦点，C₁与C₂交于M，N两点（M在第一象限），且|MF|=2．
（1）求点M的坐标及椭圆C₁的方程；
（2）若过点N且斜率为k的直线l交C₁于另一点P，交C₂于另一点Q，且MP⊥MQ，求k的值．

Answer 1

分析：（1）由抛物线方程可求得p值，设M（x₀，y₀），由抛物线定义及|MF|=2可得x₀+

p

2

=x0+1=2，解得x₀=1，进而得y₀=2，由离心率e=

3

2

及a²=b²+c²可得a，b关系，从而椭圆方程可变为含b的方程，把M坐标代入即可求得b值，进而得到a值；
（2）点N（1，-2），则直线l的方程为y+2=k（x-1），分别与椭圆方程、抛物线方程联立消掉y、x得x、y的二次方程，由韦达定理可用k表示点P、Q的坐标，从而可得向量

MP

、

MQ

的坐标，由MP⊥MQ有

MP

•

MQ

=0，得关于k的方程，解出即可；

解答：
解：（1）抛物线C₂：y²=4x，2p=4，p=2，
设M（x₀，y₀），则|MF|=x₀+

p

2

=x0+1=2，解得x₀=1，所以y₀=2，即M（1，2），
椭圆C₁：

y2

a2

+

x2

b2

=1(a＞b＞0)的离心率e=

c

a

=

3

2

，
得 

c2

a2

=

3

4

，

b2

a2

=

1

4

，a=2b，
椭圆C₁：

y2

4b2

+

x2

b2

=1过点M（1，2），所以

4

4b2

+

1

b2

=1，
求得b=

2

，a=2

2

，
所以椭圆C₁的方程是

y2

8

+

x2

2

=1．
（2）点N（1，-2），直线l的方程为y+2=k（x-1），
与C₁：y²+4x²=8，联立消去y得：4x²+（kx-k-2）²=8，
整理得（4+k²）x²-2k（k+2）x+k²+4k-4=0（i），
设P（x₁，y₁），易知1，x₁是方程（i）的两根，x₁=

k2+4k-4

4+k2

，
代入直线l的方程得y1=

2k2-8k-8

4+k2

，
y+2=k（x-1）与y²=4x联立消去x得：ky²-4y-4k-8=0（ii），
显然k≠0，设点Q（x₂，y₂），易知-2，y₂是方程（ii）的两根，-2•y₂=

-4k-8

k

，
得y2=

2k+4

k

，代入抛物线得x2=

(k+2)2

k2

，
故P(

k2+4k-4

4+k2

，

2k2-8k-8

4+k2

)，Q(

(k+2)2

k2

，

2k+4

k

)，M（1，2），

MP

=(

4k-8

4+k2

，

-8k-16

4+k2

)，

MQ

=(

4k+4

k2

，

4

k

)，
由MP⊥MQ有

MP

•

MQ

=0，即

(4k-8)(4k+4)

k2(4+k2)

+

4(-8k-16)

(4+k2)

=0，
整理得k²+5k+2=0，解得k=

-5± 17

2

．

点评：本题考查直线方程、椭圆和抛物线方程及其位置关系，考查向量的数量积运算及韦达定理的应用，考查学生综合解决问题的能力．