题目内容
已知F1、F2分别是椭圆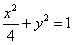 的左、右焦点,
的左、右焦点,
(Ⅰ)若P是第一象限内该椭圆上的一点,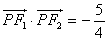 ,求点P的坐标;
,求点P的坐标;
(Ⅱ)设过定点M(0,2)的直线l与椭圆交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围。
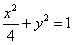 的左、右焦点,
的左、右焦点,(Ⅰ)若P是第一象限内该椭圆上的一点,
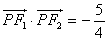 ,求点P的坐标;
,求点P的坐标;(Ⅱ)设过定点M(0,2)的直线l与椭圆交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围。
解:(Ⅰ)因为椭圆方程为 ,知
,知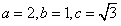 ,
,
∴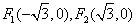 ,
,
设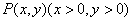 ,
,
则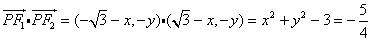 ,
,
又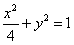 ,
,
联立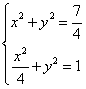 ,解得
,解得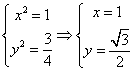 ,∴
,∴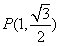 。
。
(Ⅱ)显然x=0不满足题意,可设l的方程为y=kx+2,
设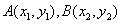 ,
,
联立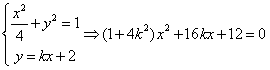 ,
,
∴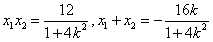 ,
,
且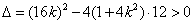 ,
,
∴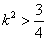 ,
,
又∠AOB为锐角,∴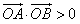 ,∴
,∴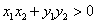 ,
,
∴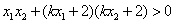 ,
,
∴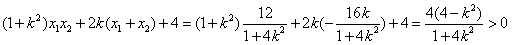 ,
,
∴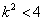 ,
,
又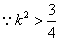 ,∴
,∴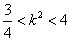 ,
,
∴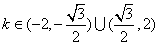 。
。

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案
相关题目
 如图,已知F1,F2分别是椭圆C:
如图,已知F1,F2分别是椭圆C: