题目内容
若向量
=(x-1 , 2),
=(y , -4)共线,则9x+3y的最小值是( )
| a |
| b |
分析:由向量共线可得2x+y=2,而9x+3y=32x+3y,由基本不等式可得答案.
解答:解:因为向量
=(x-1 , 2),
=(y , -4)共线,
所以(x-1)×(-4)-2y=0,即2x+y=2,
故9x+3y=32x+3y≥2
=2
=2
=6,
故9x+3y的最小值是6,
故选D
| a |
| b |
所以(x-1)×(-4)-2y=0,即2x+y=2,
故9x+3y=32x+3y≥2
| 32x•3y |
| 32x+y |
| 32 |
故9x+3y的最小值是6,
故选D
点评:本题考查基本不等式求最值,涉及向量的共线,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
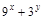 的最小值为( )
的最小值为( )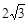 C.
C.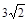 D.6
D.6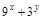 的最小值为( )
的最小值为( )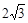 C.
C.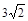 D.6
D.6