题目内容
设函数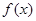 是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,
是定义在[-1,0)∪(0,1]上的奇函数,当x∈[-1,0)时,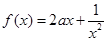 (a∈R).
(a∈R).
(1)当x∈(0,1]时,求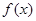 的解析式;
的解析式;
(2)若a>-1,试判断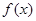 在(0,1)上的单调性,并证明你的结论;
在(0,1)上的单调性,并证明你的结论;
(3)是否存在a,使得当x∈(0,1)时,f(x)有最大值-6.
【答案】
(1)f(x)=2ax-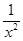 ,x∈(0,1];(2)见解析;
,x∈(0,1];(2)见解析;
(3)存在a=-2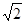 ,使f(x)在(0,1)上有最大值-6.
,使f(x)在(0,1)上有最大值-6.
【解析】(1)对于奇函数求对称区间上的解析式,根据奇函数的图像关于原点对称的特征,只须用-x,-y,分别代替原对称区间中的x,y,然后两边同乘以-1,即可得到所求区间上的解析式
(2)通过证明当a>-1时,判断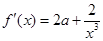 在
在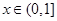 上的值的情况,进而确定f(x)在(0,1]上是否具有单调性
上的值的情况,进而确定f(x)在(0,1]上是否具有单调性
(3)本题本质是求函数f(x)在x∈(0,1)上的最大值因而,要对a进行讨论求最大值,然后利用最大值为-6,求出a值,再验证是否满意a的条件,进而判断出a值是否存在
(1)设x∈(0,1],则-x∈[-1,0),f(-x)=-2ax+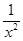 ,
,
∵f(x)是奇函数.∴f(x)=2ax-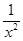 ,x∈(0,1].
,x∈(0,1].
(2)证明:∵f′(x)=2a+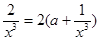 ,
,
∵a>-1,x∈(0,1],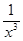 >1,∴a+
>1,∴a+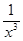 >0.即f′(x)>0.
>0.即f′(x)>0.
∴f(x)在(0,1]上是单调递增函数.
(3)解:当a>-1时,f(x)在(0,1]上单调递增.
f(x)max=f(1)=-6,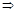 a=-
a=- (不合题意,舍之),
(不合题意,舍之),
当a≤-1时,f′(x)=0,x= .
.
如下表:fmax(x)=f( )=-6,解出a=-2
)=-6,解出a=-2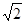 . x=
. x=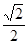 ∈(0,1).
∈(0,1).
|
|
(-∞, |
|
( |
|
|
+ |
0 |
- |
|
|
|
最大值 |
|
∴存在a=-2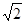 ,使f(x)在(0,1)上有最大值-6.
,使f(x)在(0,1)上有最大值-6.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
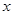
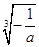 )
)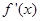
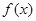

 是定义在
是定义在 上的奇函数,当
上的奇函数,当 时,
时, (a为实数).
(a为实数). 时,求
时,求 时,试判断
时,试判断 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.