题目内容
已知数列 的前
的前 项和
项和 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ) 若数列 满足
满足 ,且
,且 ,求
,求 .
.
(1)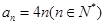 ;(2)
;(2)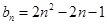
解析试题分析:(1)给出 与
与 的关系,求
的关系,求 ,常用思路:一是利用
,常用思路:一是利用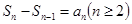 转化为
转化为 的递推关系,再求其通项公式;二是转化为
的递推关系,再求其通项公式;二是转化为 的递推关系,先求出
的递推关系,先求出 与
与 的关系,再求
的关系,再求 ;(2)数列的递推关系是给出数列的一种方法,根据给出的初始值和递推关系可以依次写出这个数列的各项,再由递推关系求数列的通项公式,常用方法有:一是求出数列的前几项,再归纳总结出数列的一个通项公式;二是将已知递推关系式整理、变形,变成等差数列或者等比数列,或用累加法,累乘法,迭代法求通项.
;(2)数列的递推关系是给出数列的一种方法,根据给出的初始值和递推关系可以依次写出这个数列的各项,再由递推关系求数列的通项公式,常用方法有:一是求出数列的前几项,再归纳总结出数列的一个通项公式;二是将已知递推关系式整理、变形,变成等差数列或者等比数列,或用累加法,累乘法,迭代法求通项.
试题解析:
解:(Ⅰ)由于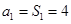
当 时,
时, 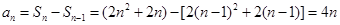
 也适合上式
也适合上式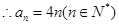 6分
6分
(Ⅱ) 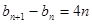 ,由累加法得
,由累加法得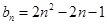 12分
12分
考点:(1)由前 项和求通项公式;(2)累加法求通项公式.
项和求通项公式;(2)累加法求通项公式.

练习册系列答案
相关题目
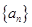 中,
中, 是其前
是其前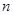 项和,
项和,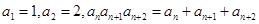 ,且
,且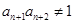 ,则
,则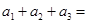 ________,
________,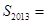 ______;
______;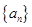 的通项公式为
的通项公式为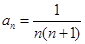 ,则该数列的前100项和为_________.
,则该数列的前100项和为_________. 满足
满足 ,
, .
. ;
; 的前n项和为
的前n项和为 ,
, ,且
,且 (
( ),数列
),数列 满足
满足 ,
, ,对任意
,对任意 。
。 .
. ;
; ,不等式
,不等式 恒成立,试求实数λ的取值范围.
恒成立,试求实数λ的取值范围.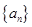 满足:
满足: .
.
 的首项
的首项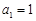 ,
, 是
是 项和,且
项和,且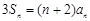
 .
.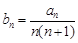 ,求数列
,求数列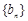 的通项公式;
的通项公式;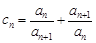 ,证明:
,证明: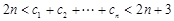 ,
,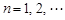 .
.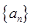 的前
的前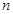 项和
项和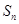 ,且满足
,且满足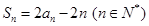 .
.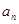 .
.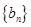 满足
满足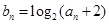 ,
,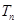 为数列{
为数列{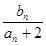 }的前
}的前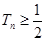 .
.