题目内容
已知函数f(x)=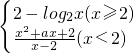 在点x=2处连续,则常数a的值是
在点x=2处连续,则常数a的值是
- A.-3
- B.3
- C.-2
- D.2
A
分析:由题意,函数在点x=2处连续即,在x=2两侧的函数值的极限相等,由此关系可判断出关于a的方程,求a
解答:∵函数f(x)=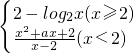 在点x=2处连续,函数值为2-log22=1,
在点x=2处连续,函数值为2-log22=1,
∴可得出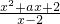 =x-1,
=x-1,
即得x2+ax+2=(x-1)(x-2)=x2-3x+2,
解得a=-3
故选A
点评:本题考查函数的连续性,求解本题关键在于理解连续性的定义,从图象上看是不间断,从定义上看是在此点两边函数的极限值相等,本题求解有一难点,即x<2时的解析没有意义,对它的处理是解题成功与否的关键,此类题在有连续性的保证下,分母一定可以约去,即分子中可以分解出一个因子,它恰好是分母,注意理解这一规律.
分析:由题意,函数在点x=2处连续即,在x=2两侧的函数值的极限相等,由此关系可判断出关于a的方程,求a
解答:∵函数f(x)=
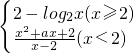 在点x=2处连续,函数值为2-log22=1,
在点x=2处连续,函数值为2-log22=1,∴可得出
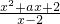 =x-1,
=x-1,即得x2+ax+2=(x-1)(x-2)=x2-3x+2,
解得a=-3
故选A
点评:本题考查函数的连续性,求解本题关键在于理解连续性的定义,从图象上看是不间断,从定义上看是在此点两边函数的极限值相等,本题求解有一难点,即x<2时的解析没有意义,对它的处理是解题成功与否的关键,此类题在有连续性的保证下,分母一定可以约去,即分子中可以分解出一个因子,它恰好是分母,注意理解这一规律.

练习册系列答案
相关题目