题目内容
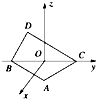 如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(
如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(
| ||
| 2 |
| 1 |
| 2 |
| OD |
分析:通过求出点D在平面yOz上坐标,利用空间直角坐标系,求出D的坐标.
解答:解:因为在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(
,
,0),
点D在平面yOz上,且∠BDC=90°,∠DCB=30°,BO=1,
所以BD=1,∠DBC=60°,D在在平面yOz上坐标(-
,
),
所以D的坐标为:(0,-
,
).
向量
的坐标为(0,-
,
).
故选B.
| ||
| 2 |
| 1 |
| 2 |
点D在平面yOz上,且∠BDC=90°,∠DCB=30°,BO=1,
所以BD=1,∠DBC=60°,D在在平面yOz上坐标(-
| 1 |
| 2 |
| ||
| 2 |
所以D的坐标为:(0,-
| 1 |
| 2 |
| ||
| 2 |
向量
| OD |
| 1 |
| 2 |
| ||
| 2 |
故选B.
点评:本题考查空间直角坐标系,求解点的坐标的求法,考查计算能力.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
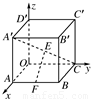
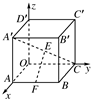 如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为( )
如图所示,在空间直角坐标系中,有一棱长为a的正方体ABCO-A′B′C′D′,A′C的中点E与AB的中点F的距离为( )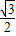 ,
, ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,则向量
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°,则向量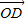 的坐标为( )
的坐标为( )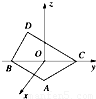
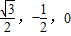 )
)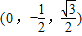
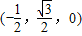
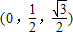
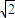 a
a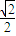 a
a a
a