题目内容
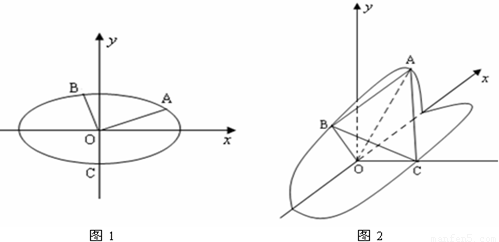
11. 如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(![]() ,
,![]() ,0),点D在平面yOz内,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz内,且∠BDC=90°,∠DCB=30°.
(1)求![]() 的坐标;
的坐标;
(2)设![]() 和
和![]() 的夹角为
的夹角为![]() ,求cos
,求cos![]() 的值.
的值.
(1)![]() 的坐标为(0,-
的坐标为(0,-![]() ,
,![]() )(2)cos
)(2)cos![]() =-
=-![]() .
.
解析:
(1)如图所示,过D作DE⊥BC,垂足为E,
在Rt△BDC中,由∠BDC=90°,∠DCB=30°,BC=2,
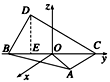 得BD=1,CD=
得BD=1,CD=![]() .
.
∴DE=CD·sin30°=![]() .
.
OE=OB-BD·cos60°=1-![]() =
=![]() .
.
∴D点坐标为(0,-![]() ,
,![]() ),
),
即![]() 的坐标为(0,-
的坐标为(0,-![]() ,
,![]() ).
).
(2)依题意:![]() =(
=(![]() ,
,![]() ,0),
,0),
![]() =(0,-1,0),
=(0,-1,0),![]() =(0,1,0).
=(0,1,0).
∴![]() =
=![]() -
-![]() =(-
=(-![]() ,-1,
,-1,![]() ),
),
![]() =
=![]() -
-![]() =(0,2,0).
=(0,2,0).
设![]() 和
和![]() 的夹角为
的夹角为![]() ,
,
则cos![]() =
=![]()
=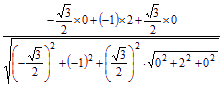
=![]() =-
=-![]() .
.
∴cos![]() =-
=-![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
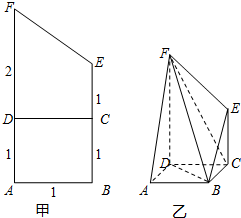 将(如图甲)直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图乙所示.
将(如图甲)直角梯形ABEF(图中数字表示对应线段的长度)沿直线CD折成直二面角,连接部分线段后围成一个空间几何体,如图乙所示.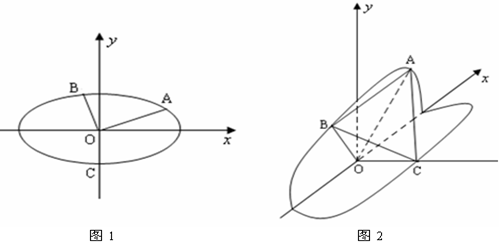
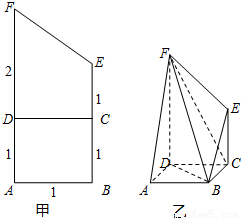
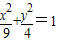 的下顶点为C,A,B分别在椭圆的第一象限和第二象限的弧上运动,满足
的下顶点为C,A,B分别在椭圆的第一象限和第二象限的弧上运动,满足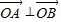 ,其中O为坐标原点,现沿x轴将坐标平面折成直二面角.如图2所示,在空间中,解答下列问题:
,其中O为坐标原点,现沿x轴将坐标平面折成直二面角.如图2所示,在空间中,解答下列问题: