题目内容
12.在下列四个命题中:①函数y=sin2x+2cos2x最小正周期是π;
②若向量$\overrightarrow{a}$∥$\overrightarrow{m}$,$\overrightarrow{b}$∥$\overrightarrow{m}$,则$\overrightarrow{a}$∥$\overrightarrow{b}$;
③在△ABC中,M是BC的中点,AM=3,点P在AM上且满足$\overrightarrow{AP}$=2$\overrightarrow{PM}$,则$\overrightarrow{PA}$•($\overrightarrow{PB}$+$\overrightarrow{PC}$)=-4;
④函数(x)=xsinx在区间[0,$\frac{π}{2}$]上单调递增,在区间[-$\frac{π}{2}$,0]函数f(x)上单调递减.
把你认为正确的命题的序号都填在横线上①,③,④.
分析 (1)考察同角三角函数的转换和周期的判断
(2)是向量的基本概念,属于基础题型
(3)向量的加法和数量积,结合图形分析
(4)考察复合函数单调性的判断.
解答  解:(1)y=1+cos2x=$\frac{1}{2}$cos2x+$\frac{3}{2}$,
解:(1)y=1+cos2x=$\frac{1}{2}$cos2x+$\frac{3}{2}$,
∴T=π,真命题
(2)零向量与任一向量共线,当向量m为零向量时不成立.假命题
(3)如图:$\overrightarrow{PB}$+$\overrightarrow{PC}$=2$\overrightarrow{PM}$=$\overrightarrow{AP}$
∴$\overrightarrow{PA}$•$\overrightarrow{AP}$=-$\overrightarrow{AP}$2=-4 真命题
(4)f′(x)=sinx+cosx•x
f′(0)=0
当x∈[0,$\frac{π}{2}$]时,f′(x)≥0,f(x)单调递增
当x∈[-$\frac{π}{2}$,0]时,f′(x)≤0,f(x)单调递减
故答案为:①,③,④.
点评 分别考察了三角函数的转换和向量的运算.是常规题型,应掌握解题方法.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目

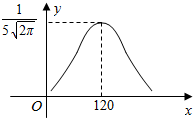 已知随机变量X的概率密度曲线如图所示:
已知随机变量X的概率密度曲线如图所示: