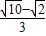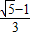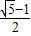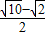Question

以正方形ABCD的相对顶点A、C为焦点的椭圆，恰好过正方形四边的中点，则该椭圆的离心率为（　　）

• A、

  10 - 2

  3

• B、

  5 -1

  3

• C、

  5 -1

  2

• D、

  10 - 2

  2

Answer 1

分析：设正方形边长为2，设正方形中心为原点，设椭圆的标准方程，则可知c，的a和b的关系式，进而求得BC的中点坐标代入椭圆方程，得到a和b的另一关系式，最后联立求得a，则椭圆的离心率可得．

解答：解：设正方形边长为2，设正方形中心为原点
则椭圆方程为

x2

a2

+

y2

b2

 =1
且c=

2

∴a²-b²=c²=2①
正方形BC边的中点坐标为（

1

2

，

1

2

）
代入方程得到

1

2a2

+

1

2b2

=1②
联立①②解得a=

1+ 5

2

∴e=

c

a

=

10 - 2

2

．
故选D．

点评：本题主要考查了椭圆的简单性质．要求学生熟练掌握椭圆标准方程中，a，b和c及离心率e的关系．