题目内容
((本题14分)定义:若函数 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且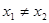 ,都有
,都有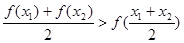 ,则称函数
,则称函数 在区间D上具有性质L。
在区间D上具有性质L。
(1)写出一个在其定义域上具有性质L的对数函数(不要求证明)。
(2)对于函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。
(3)若函数 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数 的取值范围。
的取值范围。
【答案】
解:(1) (或其它底在(0,1)上的对数函数)。…………2分
(或其它底在(0,1)上的对数函数)。…………2分
(2)函数 在区间
在区间 上具有性质L。…………4分
上具有性质L。…………4分
证明:任取 、
、 ,且
,且
则



 、
、 且
且 ,
,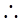
 ,
,
即 >0,
>0,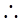

所以函数 在区间
在区间 上具有性质L。……………8分
上具有性质L。……………8分
(3)任取 、
、 ,且
,且
则




 、
、 且
且 ,
,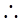
 ,
,
要使上式大于零,必须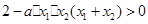 在
在 、
、 上恒成立,
上恒成立,
即 ,
,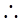
 ,即实数
,即实数 的取值范围为
的取值范围为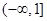 ……………14分
……………14分
【解析】略

练习册系列答案
相关题目

 在某一区间D上任取两个实数
在某一区间D上任取两个实数 、
、 ,且
,且 ,都有
,都有 ,则称函数
,则称函数 ,判断其在区间
,判断其在区间 上是否具有性质L?并用所给定义证明你的结论。
上是否具有性质L?并用所给定义证明你的结论。 在区间(0,1)上具有性质L,求实数
在区间(0,1)上具有性质L,求实数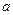 的取值范围。
的取值范围。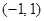 上的函数
上的函数 满足:
满足: ,都有
,都有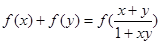
 时,有
时,有 ,求证:(Ⅰ)
,求证:(Ⅰ) 是奇函数;
是奇函数;
 ,求数列{an}的通项公式,并求所有可能乘积aiaj(1≤i≤j≤n)的和.
,求数列{an}的通项公式,并求所有可能乘积aiaj(1≤i≤j≤n)的和.