题目内容
(本小题满分12分)
如图,在四棱锥P-ABCD中,底面为正文形,PA 平面ABCD,且PA=AD,E为棱PC上的一点,PD
平面ABCD,且PA=AD,E为棱PC上的一点,PD 平面ABE
平面ABE
(I)求证:E为PC的中点
(II)若N为CD中点,M为AB上的动点,当直线MN与平面ABE所成的角最大时,求二面角C-EM—N的大小

【答案】
解:(Ⅰ)过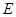 作
作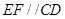 交
交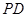 于
于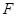 ,由
,由
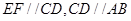 可知
可知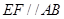
 四点共面,…………………2分
四点共面,…………………2分
又因为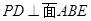
∴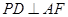 ,
,
∵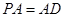
∴在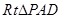 中,
中,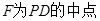 ,………………………4分
,………………………4分
∴可得E为PC的中点.……………………6分
(Ⅱ)连结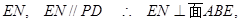
连结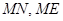 ,则
,则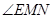 为直线MN与平面ABE所成的角.
为直线MN与平面ABE所成的角.
在
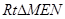 中,
中,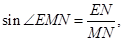
∴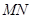 最小时,
最小时,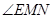 最大,此时
最大,此时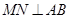 .
.
所以M为AB中点,……………………………9分
则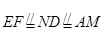 .
.
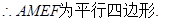 由
由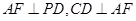 ,
,
可知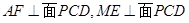
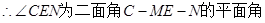
设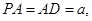
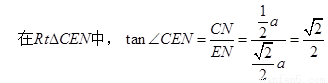 ,
,

 .……………12分
.……………12分
法二(Ⅰ)建立如图所示空间直角坐标系,不妨设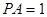 ,则
,则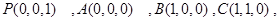
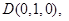
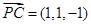 ,
,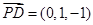 .………………2分
.………………2分
设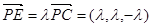 ,
,
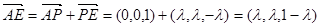 ,…………………4分
,…………………4分
因为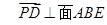 ,
, 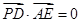 ,
,
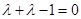 ,
,
即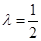 ,
,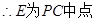 .……………………6分
.……………………6分
(Ⅱ)设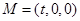 ,
,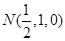 ,
,
由(Ⅰ)知面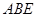 的法向量为
的法向量为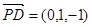 ,
,
设MN与面ABE所成角为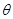 ,
,
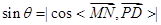
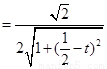
当t=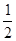 时,
时,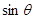 最大,此时M为AB中点,…………………9分
最大,此时M为AB中点,…………………9分
平面NEM的法向量为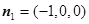 设平面CEM的法向量为
设平面CEM的法向量为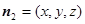
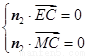 而
而 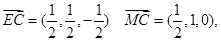
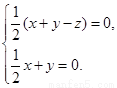 令
令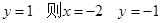 .
.
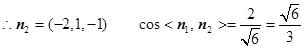 ,
,
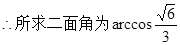 .……………………12分
.……………………12分
【解析】略

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目