题目内容
已知x,y,z满足(x-3)2+(y-4)2+z2=2,那么x2+y2+z2的最小值是
27-10
| 2 |
27-10
.| 2 |
分析:利用球心与坐标原点的距离减去半径即可求出表达式的最小值.
解答:解:由题意可得P(x,y,z),在以M(3,4,0)为球心,
为半径的球面上,
x2+y2+z2表示原点与点P的距离的平方,
显然当O,P,M共线且P在O,M之间时,|OP|最小,
此时|OP|=|OM|-
=
-
=5
,
所以|OP|2=27-10
.
故答案为:27-10
.
| 2 |
x2+y2+z2表示原点与点P的距离的平方,
显然当O,P,M共线且P在O,M之间时,|OP|最小,
此时|OP|=|OM|-
| 2 |
| 32+42 |
| 2 |
| 2 |
所以|OP|2=27-10
| 2 |
故答案为:27-10
| 2 |
点评:本题考查空间中两点间的距离公式的应用,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知x,y,z满足方程x2+(y-2)2+(z+2)2=2,则
的最大值是( )
| x2+y2+z2 |
A、3
| ||
B、2
| ||
C、4
| ||
D、
|
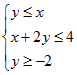 , 则t=x2+y2+2x-2y+2的最小值为( )
, 则t=x2+y2+2x-2y+2的最小值为( )