题目内容
若函数 的导函数在区间
的导函数在区间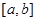 上是增函数,则函数
上是增函数,则函数 在区间
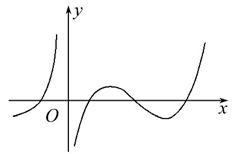
在区间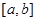 上的图象可能是( )
上的图象可能是( )
A
解析试题分析:∵函数y=f(x)的导函数在区间[a,b]上是增函数,∴对任意的a<x1<x2<b,有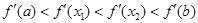 也即在a,x1,x2,b处它们的斜率是依次增大的.∴A 满足上述条件,
也即在a,x1,x2,b处它们的斜率是依次增大的.∴A 满足上述条件,
对于B 存在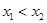 使
使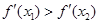 ,对于C 对任意的a<x1<x2<b,都有
,对于C 对任意的a<x1<x2<b,都有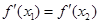 ,对于D 对任意的x∈[a,b],
,对于D 对任意的x∈[a,b],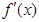 不满足逐渐递增的条件,故选A.
不满足逐渐递增的条件,故选A.
考点:单调性与导函数的关系.

练习册系列答案
相关题目
已知 是定义在
是定义在 上的偶函数,且
上的偶函数,且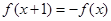 ,若
,若 在
在 上单调递减,则
上单调递减,则 在
在 上是( )
上是( )
| A.增函数 | B.减函数 |
| C.先增后减的函数 | D.先减后增的函数 |
下列函数中,满足“ ”的单调递增函数是( )
”的单调递增函数是( )
A. | B. | C. | D. |
已知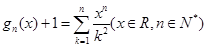 ,则下列说法正确的是( )
,则下列说法正确的是( )
①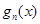 关于点
关于点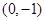 成中心对称
成中心对称
②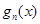 在
在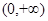 单调递增
单调递增
③当 取遍
取遍 中所有数时不可能存在
中所有数时不可能存在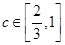 使得
使得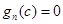
| A.①②③ | B.②③ | C.①③ | D.② |
 p:
p: ,q:
,q: .
. 的取值范围;
的取值范围;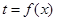 的图像大致为( )
的图像大致为( )
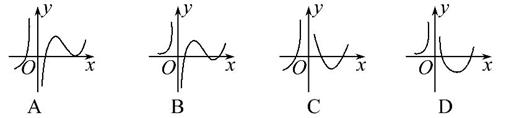
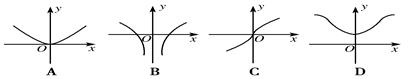
 |≤2,q::x2-2x+1-m2≤0(m>0),若
|≤2,q::x2-2x+1-m2≤0(m>0),若 是
是 的必要而不充分条件,求实数m的取值范围. ks*5*u
的必要而不充分条件,求实数m的取值范围. ks*5*u