题目内容
(1)是否存在正整数的无穷数列{an},使得对任意的正整数n都有an+12≥2anan+2.
(2)是否存在正无理数的无穷数列{an},使得对任意的正整数n都有an+12≥2anan+2.
解:(1)假设存在正整数数列{an}满足条件.
∵an+12≥2anan+2,an>0,∴ ,…
,…
又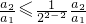 ,所以有
,所以有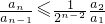 对n=2,3,4,成立.
对n=2,3,4,成立.
∴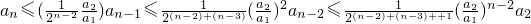
所以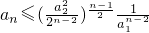 .
.
设a22∈[2k,2k+1),k∈N,取N=k+3,则有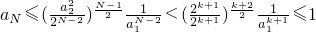 ,
,
这与aN是正整数矛盾.
所以不存在正整数数列{an}满足条件.
(2)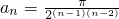 就是满足条件的一个无理数数列.此时有an+12=4anan+2≥2anan+2.
就是满足条件的一个无理数数列.此时有an+12=4anan+2≥2anan+2.
分析:(1)假设存在正整数数列{an}满足条件,即an+12≥2anan+2,an>0,整式化为分式,得到 …,即
…,即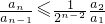 ,进一步论证即可说明不存在;
,进一步论证即可说明不存在;
(2)举例说明即可,如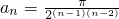 ,代入an+12≥2anan+2进行验证即可.
,代入an+12≥2anan+2进行验证即可.
点评:此题是个中档题.考查学生灵活应用知识分析、解决问题的能力,特别是问题(1)的设问形式,增加了题目的难度,对学生的逻辑思维要求特别高,灵活性强.
∵an+12≥2anan+2,an>0,∴
 ,…
,…又
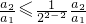 ,所以有
,所以有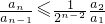 对n=2,3,4,成立.
对n=2,3,4,成立.∴
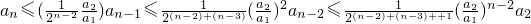
所以
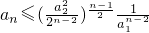 .
.设a22∈[2k,2k+1),k∈N,取N=k+3,则有
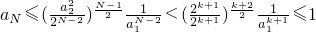 ,
,这与aN是正整数矛盾.
所以不存在正整数数列{an}满足条件.
(2)
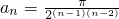 就是满足条件的一个无理数数列.此时有an+12=4anan+2≥2anan+2.
就是满足条件的一个无理数数列.此时有an+12=4anan+2≥2anan+2.分析:(1)假设存在正整数数列{an}满足条件,即an+12≥2anan+2,an>0,整式化为分式,得到
 …,即
…,即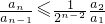 ,进一步论证即可说明不存在;
,进一步论证即可说明不存在;(2)举例说明即可,如
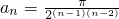 ,代入an+12≥2anan+2进行验证即可.
,代入an+12≥2anan+2进行验证即可.点评:此题是个中档题.考查学生灵活应用知识分析、解决问题的能力,特别是问题(1)的设问形式,增加了题目的难度,对学生的逻辑思维要求特别高,灵活性强.

练习册系列答案
相关题目