题目内容
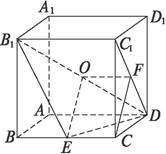
已知棱长为a的正方体ABCD—A1B1C1D1,E为BC中点.
(1)求B到平面B1ED距离
(2)求直线DC和平面B1ED所成角的正弦值. (12分) 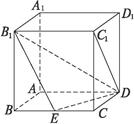
(1) d =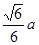 ;(2)sinα=
;(2)sinα=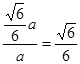 。
。
解析试题分析:(1)求点到平面的距离,可利用体积法.可利用V B1-ECD=V C-B1DE.
(2)因为E为BC的中点,所以点C到平面B1ED的距离等于点B到平面B1ED的距离h,在(I)的基础上可求出直线DC和平面B1ED所成角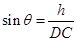 .
.
(1)以A为原点,AB,AD,AA为x轴,y轴,z轴建立坐标系如图.用向量法易求得B到平面B1ED距离d =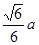
(2)方法一:向量法略
方法二:解:在四面体B1—DCE中,V B1—ECD=V C—B1DE,
则S△B1DE·h C—B1DE=S△ECD·h B1—ECD
而S B1DE=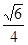 a2,S△ECD=
a2,S△ECD=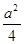 ,则h C—B1DE=
,则h C—B1DE=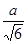 .
.
则sinα=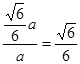
考点:点到平面的距离,直线与平面所成的角.
点评:利用四面体可换底的特性,求出点到平面的距离.求线面角如果直接找角不好找,可以象本题一样转化为点到平面的距离求解.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
 中,棱长
中,棱长 ,
, 、
、 分别为
分别为 、
、 的中点,
的中点, 、
、 是
是 、
、 的中点,
的中点,
 //平面
//平面 ;
; 到平面
到平面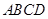 中,
中,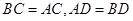 ,
,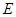 是
是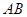 的中点.
的中点.
 平面
平面 ;
;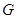 为
为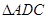 的重心,
的重心,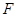 是线段
是线段 上一点,且
上一点,且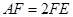 .求证:
.求证: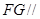 平面
平面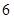 ,在四棱锥
,在四棱锥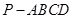 中,
中,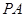
 平面
平面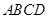 ,底面
,底面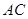 与
与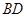 的交点,
的交点,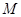 是
是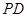 的中点,
的中点,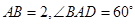 .
.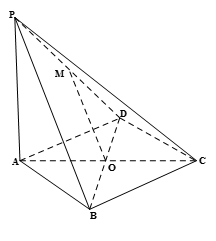
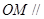 平面
平面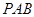 ;
;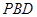
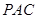 ;
;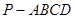 的体积等于
的体积等于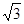 时,求
时,求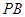 的长.
的长.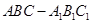 (侧棱垂直于底面的棱柱)中,
(侧棱垂直于底面的棱柱)中,  ,
, 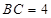 ,
, 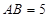 ,
,  ,点
,点 是
是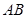 的中点.
的中点. 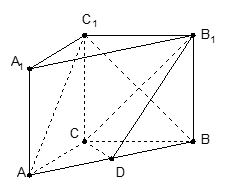
 ∥平面
∥平面 ;
;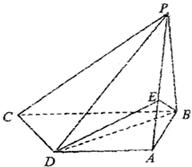
 中,
中,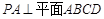 ,
,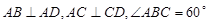 ,且
,且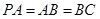 ,E是PC的中点.
,E是PC的中点.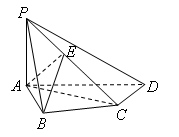
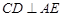 ;
; 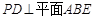 ;
;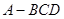 中,面
中,面 面
面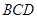 ,
,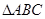 是正三角形,
是正三角形,  ,
,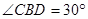 .
.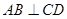 ;
; 与
与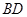 所成角的余弦值.
所成角的余弦值.
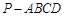 的底面是直角梯形,
的底面是直角梯形,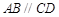 ,
, ,
, 和
和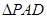 是两个边长为
是两个边长为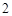 的正三角形,
的正三角形,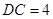 ,
,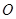 为
为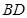 的中点,
的中点,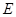 为
为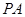 的中点.
的中点.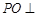 平面
平面 ;
;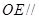 平面
平面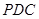 ;
;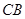 与平面
与平面