Question

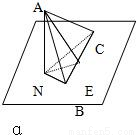
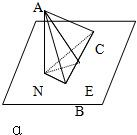如图，已知一块直角三角形板ABC的BC边在平面α内，∠ABC=60°，∠ACB=30°，BC=24cm，A点在平面α内的射影为N，AN=9cm，求以A为顶点的三棱锥A-NBC的体积（结果可以保留根号）．

Answer 1

分析：过N作NE⊥BC，E为垂足，连接AE，求出AE，NE，求出底面△NBC面积，然后求出体积即可．

解答：解：过N作NE⊥BC，E为垂足，连接AE，
由三垂线定理可知AE⊥BC
在直角三角形ABC中，
AE=BC•sin30°•sin60°=6

3

．
在直角三角形ANE中，
NE=

AE2-AN2

=3

3

．
△NBC的面积S=

1

2

•BC•NE=36

3

三棱锥A-NBC的体积V=

1

3

•S•AN=108

3

(cm2)
答：三棱锥A-NBC的体积为：108

3

cm²

点评：本题考查线线关系证明垂直关系，从而说明锥体的高，求出底面面积是解好本题的一个环节，考查计算能力，是基础题．