题目内容
甲、乙两人进行射击训练,命中率分别为 与P,且乙射击2次均未命中的概率为
与P,且乙射击2次均未命中的概率为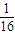 ,
,(I)求乙射击的命中率;
(Ⅱ)若甲射击2次,乙射击1次,两人共命中的次数记为ξ,求ξ的分布列和数学期望.
【答案】分析:(I)设“甲射击一次命中”为事件A,“乙射击一次命中”为事件B,由题意得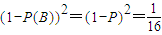 ,解方程即可求解
,解方程即可求解
(II)由题意和(I)知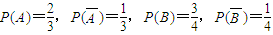 .,ξ可能的取值为0,1,2,3,根据相互独立事件的概率公式求解出每种情况下的概率即可求得ξ的分布列,进而可求期望值
.,ξ可能的取值为0,1,2,3,根据相互独立事件的概率公式求解出每种情况下的概率即可求得ξ的分布列,进而可求期望值
解答:解:(I)设“甲射击一次命中”为事件A,“乙射击一次命中”为事件B
由题意得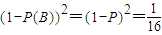 ┉┉┉┉┉┉┉┉┉┉(4分)
┉┉┉┉┉┉┉┉┉┉(4分)
解得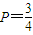 或
或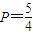 (舍去),┉┉┉┉┉┉┉┉┉┉(5分)
(舍去),┉┉┉┉┉┉┉┉┉┉(5分)
故乙射击的命中率为 .┉┉┉┉┉┉┉┉┉┉(6分)
.┉┉┉┉┉┉┉┉┉┉(6分)
(II)由题意和(I)知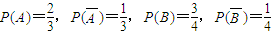 .
.
ξ可能的取值为0,1,2,3,
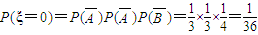 ┉┉┉┉┉┉┉┉┉┉(7分)
┉┉┉┉┉┉┉┉┉┉(7分)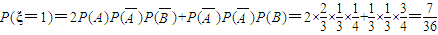 .(8分)
.(8分)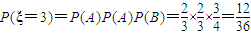 ┉┉┉┉┉┉┉┉┉┉(9分)
┉┉┉┉┉┉┉┉┉┉(9分)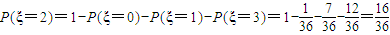 ┉┉┉(10分)
┉┉┉(10分)
故ξ的分布列为
由此得ξ的数学期望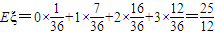 ┉┉┉(12分)
┉┉┉(12分)
点评:本题主要考查了相互独立事件的概率公式的应用,离散型随机变量的分布列及期望值的求解.
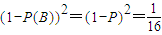 ,解方程即可求解
,解方程即可求解(II)由题意和(I)知
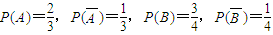 .,ξ可能的取值为0,1,2,3,根据相互独立事件的概率公式求解出每种情况下的概率即可求得ξ的分布列,进而可求期望值
.,ξ可能的取值为0,1,2,3,根据相互独立事件的概率公式求解出每种情况下的概率即可求得ξ的分布列,进而可求期望值解答:解:(I)设“甲射击一次命中”为事件A,“乙射击一次命中”为事件B
由题意得
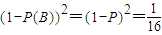 ┉┉┉┉┉┉┉┉┉┉(4分)
┉┉┉┉┉┉┉┉┉┉(4分)解得
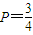 或
或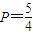 (舍去),┉┉┉┉┉┉┉┉┉┉(5分)
(舍去),┉┉┉┉┉┉┉┉┉┉(5分)故乙射击的命中率为
 .┉┉┉┉┉┉┉┉┉┉(6分)
.┉┉┉┉┉┉┉┉┉┉(6分)(II)由题意和(I)知
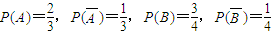 .
.ξ可能的取值为0,1,2,3,
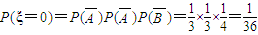 ┉┉┉┉┉┉┉┉┉┉(7分)
┉┉┉┉┉┉┉┉┉┉(7分)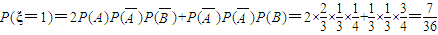 .(8分)
.(8分)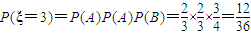 ┉┉┉┉┉┉┉┉┉┉(9分)
┉┉┉┉┉┉┉┉┉┉(9分)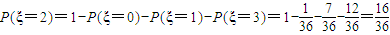 ┉┉┉(10分)
┉┉┉(10分)故ξ的分布列为
| ξ | 1 | 2 | 3 | |
| P | 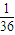 | 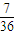 | 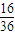 |  |
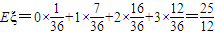 ┉┉┉(12分)
┉┉┉(12分)点评:本题主要考查了相互独立事件的概率公式的应用,离散型随机变量的分布列及期望值的求解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目