题目内容
(本小题满分12分)
已知函数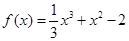 。
。
(Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3,若点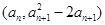 (n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;
(Ⅱ)求函数f(x)在区间(a-1,a)内的极值。
【答案】
(Ⅰ)证明见解析。
(Ⅱ)当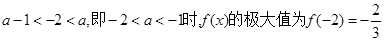 ,此时
,此时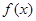 无极小值;
无极小值;
当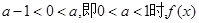 的极小值为
的极小值为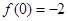 ,此时
,此时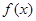 无极大值;
无极大值;
当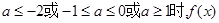 既无极大值又无极小值。
既无极大值又无极小值。
【解析】(Ⅰ)证明:因为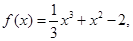 所以
所以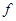 ′(x)=x2+2x,
′(x)=x2+2x,
由点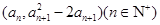 在函数y=f′(x)的图象上,
在函数y=f′(x)的图象上,
又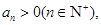 所以
所以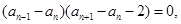
所以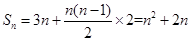 ,又因为
,又因为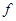 ′(n)=n2+2n,所以
′(n)=n2+2n,所以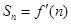 ,
,
故点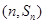 也在函数y=f′(x)的图象上.
也在函数y=f′(x)的图象上.
(Ⅱ)解: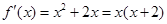 ,
,
由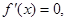 得
得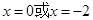 .
.
当x变化时,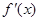 ﹑
﹑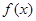 的变化情况如下表:
的变化情况如下表:
|
x |
(-∞,-2) |
-2 |
(-2,0) |
0 |
(0,+∞) |
|
f′(x) |
+ |
0 |
- |
0 |
+ |
|
f(x) |
↗ |
极大值 |
↘ |
极小值 |
↗ |
注意到 ,从而
,从而
①当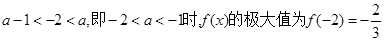 ,此时
,此时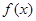 无极小值;
无极小值;
②当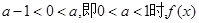 的极小值为
的极小值为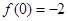 ,此时
,此时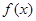 无极大值;
无极大值;
③当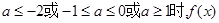 既无极大值又无极小值。
既无极大值又无极小值。

练习册系列答案
相关题目