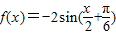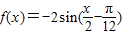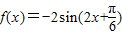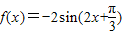题目内容
将函数f(x)图象沿x轴向右平移
个单位长度,再将所得图象上的每一点的横坐标伸长到原来的2倍、纵坐标保持不变,这样得到的是函数y=-2sinx的图象,那么f(x)的解析式是( )
| π |
| 6 |
分析:按照函数的图象平移变换逆向推导,即可得到f(x)的解析式.
解答:解:由题意将函数f(x)图象沿x轴向右平移
个单位长度,再将所得图象上的每一点的横坐标伸长到原来的2倍、
纵坐标保持不变,这样得到的是函数y=-2sinx的图象,
所以函数y=-2sinx的图象每一点的横坐标伸缩到原来的
倍、纵坐标保持不变,
得到函数y=-2sin2x,图象沿x轴向左平移
个单位长度,得到函数y=-2sin2(x+
),
即函数解析式为:f(x)=-2sin(2x+
).
故选D.
| π |
| 6 |
纵坐标保持不变,这样得到的是函数y=-2sinx的图象,
所以函数y=-2sinx的图象每一点的横坐标伸缩到原来的
| 1 |
| 2 |
得到函数y=-2sin2x,图象沿x轴向左平移
| π |
| 6 |
| π |
| 6 |
即函数解析式为:f(x)=-2sin(2x+
| π |
| 3 |
故选D.
点评:本题考查函数的图象的平移与伸缩变换,注意变换的逆应用,考查计算能力.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若函数f(x)图象上每一个点的纵坐标保持不变,横坐标伸长到原来的两倍,然后再将整个图象沿x轴向右平移
个单位,向下平移3个单位,恰好得到函数y=
sinx的图象,则函数f(x)的解析式为( )
| π |
| 2 |
| 1 |
| 2 |
A、f(x)=
| ||||||
B、f(x)=-
| ||||||
C、f(x)=
| ||||||
D、f(x)=
|
 个单位长度,再将所得图象上的每一点的横坐标伸长到原来的2倍、纵坐标保持不变,这样得到的是函数y=-2sinx的图象,那么f(x)的解析式是
个单位长度,再将所得图象上的每一点的横坐标伸长到原来的2倍、纵坐标保持不变,这样得到的是函数y=-2sinx的图象,那么f(x)的解析式是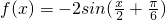
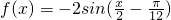
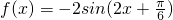
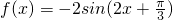
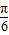 个单位长度,再将所得图象上的每一点的横坐标伸长到原来的2倍、纵坐标保持不变,这样得到的是函数y=-2sinx的图象,那么f(x)的解析式是( )
个单位长度,再将所得图象上的每一点的横坐标伸长到原来的2倍、纵坐标保持不变,这样得到的是函数y=-2sinx的图象,那么f(x)的解析式是( )