题目内容
有下列两个命题:
命题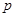 :对
:对 ,
,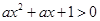 恒成立。
恒成立。
命题 :函数
:函数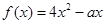 在
在 上单调递增。
上单调递增。
若“ ”为真命题,“
”为真命题,“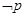 ”也为真命题,求实数
”也为真命题,求实数 的取值范围。
的取值范围。
命题
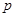 :对
:对 ,
,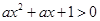 恒成立。
恒成立。命题
 :函数
:函数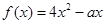 在
在 上单调递增。
上单调递增。若“
 ”为真命题,“
”为真命题,“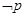 ”也为真命题,求实数
”也为真命题,求实数 的取值范围。
的取值范围。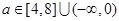
试题分析:(1)对
 ,
,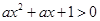 恒成立,当
恒成立,当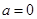 时显然成立;
时显然成立;当
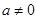 时,必有
时,必有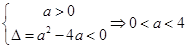 ,所以命题
,所以命题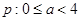
函数
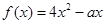 在
在 上单调递增
上单调递增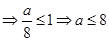 ,所以命题
,所以命题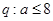
由已知:
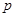 假
假 真,所以
真,所以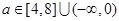
点评:典型题,涉及命题的题目,往往综合性较强。
 是真命题,意味着p,q至少有一是真命题,
是真命题,意味着p,q至少有一是真命题,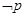 是真命题,p一定是假命题。
是真命题,p一定是假命题。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
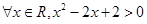 ”的否定是 .
”的否定是 .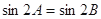 ,则
,则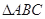 是等腰三角形;②若
是等腰三角形;②若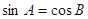 ,则
,则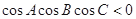 ,则
,则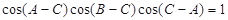 ,则
,则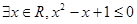 ;
;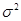 ),P(X≤6)=0.72,则P(X≤0)=0.28;
),P(X≤6)=0.72,则P(X≤0)=0.28;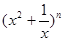 的展开式的各项系数和为32,则展开式中x项的系数为20;
的展开式的各项系数和为32,则展开式中x项的系数为20;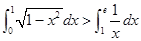
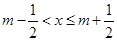 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m,在此基础上给出关于函数
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m,在此基础上给出关于函数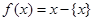 的四个命题:
的四个命题: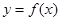 的定义域是R,值域为
的定义域是R,值域为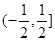 ;
;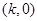 是
是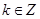 ;
; 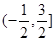 上是增函数.
上是增函数.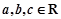 ,有下列命题:
,有下列命题: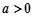 ,则
,则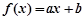 在
在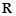 上是单调函数;
上是单调函数;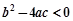 ,则
,则 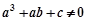 ;
;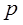 ,
,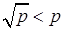 ;
;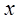 ,使
,使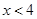 且
且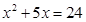 ;
;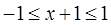 且
且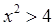 ;
;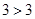 ,
,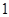
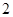
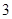
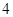
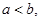 则
则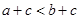 ”. ( 其中
”. ( 其中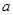 、
、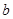 、
、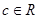 )
)