题目内容
点P在双曲线上，F1，F2为焦点，且PF1⊥PF2，|PF1|=3|PF2|则其离心率为（ ）A．
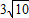
B．
C．
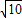
D．
【答案】分析：根据双曲线的定义，即勾股定理，可确定几何量之间的关系，从而可求双曲线的离心率．
解答：解：设|PF2|=m，则|PF1|=3m
∴|PF1|-|PF2|=2a=2m
∴m=a
∵PF1⊥PF2，|
∴9m2+m2=4c2
∴10m2=4c2
∴10a2=4c2
∴e=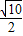
故选D．
点评：本题考查双曲线的定义，考查双曲线的几何性质，解题的关键是确定几何量之间的关系．
解答：解：设|PF2|=m，则|PF1|=3m
∴|PF1|-|PF2|=2a=2m
∴m=a
∵PF1⊥PF2，|
∴9m2+m2=4c2
∴10m2=4c2
∴10a2=4c2
∴e=
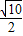
故选D．
点评：本题考查双曲线的定义，考查双曲线的几何性质，解题的关键是确定几何量之间的关系．
练习册系列答案
相关题目
上，F1，F2是这条双曲线的两个焦点，∠F1PF2＝90°，且△F1PF2的三条边长成等差数列，则此双曲线的离心率是
上，F1、F2是这条双曲线的两个焦点，
，且△F1PF2的三条边长成等差数列，则此双曲线的离心率等于（ ）