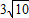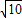题目内容
点P在双曲线
上，F1、F2是这条双曲线的两个焦点，
，且△F1PF2的三条边长成等差数列，则此双曲线的离心率等于（ ）A．3
B．4
C．5
D．6
【答案】分析：设|PF2|，|PF1|，|F1F2|成等差数列，且分别设为m-d，m，m+d，则由双曲线定义和勾股定理求出m=4d=8a，
c=
，由此求得离心率的值．
解答：解：设|PF2|，|PF1|，|F1F2|成等差数列，且分别设为m-d，m，m+d，
则由双曲线定义和勾股定理可知：m-（m-d）=2a，m+d=2c，（m-d）2+m2=（m+d）2，
解得m=4d=8a，c=
，故离心率
，
故选 C．
点评：本题主要考查等差数列的定义和性质，以及双曲线的简单性质的应用，属于中档题．
c=
，由此求得离心率的值．解答：解：设|PF2|，|PF1|，|F1F2|成等差数列，且分别设为m-d，m，m+d，
则由双曲线定义和勾股定理可知：m-（m-d）=2a，m+d=2c，（m-d）2+m2=（m+d）2，
解得m=4d=8a，c=
，故离心率，故选 C．
点评：本题主要考查等差数列的定义和性质，以及双曲线的简单性质的应用，属于中档题．
练习册系列答案
黄冈创优卷系列答案
相关题目
上，F1，F2是这条双曲线的两个焦点，∠F1PF2＝90°，且△F1PF2的三条边长成等差数列，则此双曲线的离心率是
