题目内容
在以下四组函数中,表示同一个函数的是( )A.f(x)=x+1,
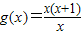
B.f(x)=1,
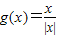
C.y=f(x),y=f(t)
D.f(x)=x2+1,g(x)=x2
【答案】分析:只有定义域完全一致,对应法则完全相同的函数才能表示同一函数,由此进行判断能求出结果.
解答:解:∵f(x)=x+1的定义域是R, 的定义域是x≠0,
的定义域是x≠0,
∴f(x)=x+1与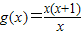 不能表示同一函数;
不能表示同一函数;
∵f(x)=1的定义域是R,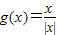 的定义域是x≠0,
的定义域是x≠0,
∴f(x)=1和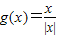 不能表示同一函数;
不能表示同一函数;
∵y=f(x)与y=f(t)的定义域和对应法则完全一致,
∴y=f(x)和y=f(t)表示同一函数;
∵f(x)=x2+1和g(x)=x2对应法则不一致,
∴f(x)=x2+1和g(x)=x2不能表示同一函数.
故选C.
点评:本题考查同一函数的判断和应用,解题时要认真审题,注意等价转化思想的合理运用.
解答:解:∵f(x)=x+1的定义域是R,
 的定义域是x≠0,
的定义域是x≠0,∴f(x)=x+1与
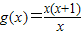 不能表示同一函数;
不能表示同一函数;∵f(x)=1的定义域是R,
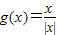 的定义域是x≠0,
的定义域是x≠0,∴f(x)=1和
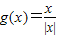 不能表示同一函数;
不能表示同一函数;∵y=f(x)与y=f(t)的定义域和对应法则完全一致,
∴y=f(x)和y=f(t)表示同一函数;
∵f(x)=x2+1和g(x)=x2对应法则不一致,
∴f(x)=x2+1和g(x)=x2不能表示同一函数.
故选C.
点评:本题考查同一函数的判断和应用,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
在以下四组函数中,表示相等函数的是( )
A、f(x)=x+1,g(x)=
| |||||
| B、f(x)=1,g(x)=x0 | |||||
C、f(x)=5x+
| |||||
D、f(x)=
|