题目内容
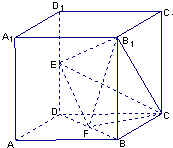 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
(1)求证:EF∥面ABC1D1
(2)求证EF∥BD1.
(3)求三棱锥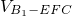 的体积.
的体积.
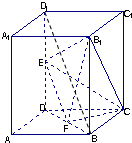 证明:(1)∵E、F分别为DD1、BD的中点
证明:(1)∵E、F分别为DD1、BD的中点∴EF∥BD1且EF=
 BD1
BD1∵BD1?平面ABC1D1且EF?平面ABC1D1
∴EF∥面ABC1D1
(2))∵E、F分别为DD1、BD的中点
∴EF∥BD1
(3)∵在正方体ABCD-A1B1C1D1中
∴B1C⊥BC1,B1C⊥C1D1
∴B1C⊥平面BC1D1
∴B1C⊥BD1
∵EF∥BD1
∴B1C⊥EF
又∵EF⊥FC
∴EF⊥平面FCB1
∵EF=
 BD1
BD1∴EF=

∵FC⊥平面BDD1B1
∴FC⊥FB1
又∵在棱长为2的正方体中
∴FC=
 ,FB1=
,FB1=
∴
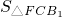 =
=
∴
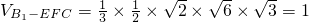
所以三棱锥
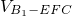 的体积为1..
的体积为1..分析:(1)E、F分别为DD1、BD的中点,所以EF∥BD1且EF=
 BD1.又因为BD1?平面ABC1D1且EF?平面ABC1D1所以EF∥面ABC1D1
BD1.又因为BD1?平面ABC1D1且EF?平面ABC1D1所以EF∥面ABC1D1(2)E、F分别为DD1、BD的中点∴EF∥BD1
(3)B1C⊥EF且EF⊥FC所以EF⊥平面FCB1,所以EF=
 ,因为FC=
,因为FC= ,FB1=
,FB1= 所以
所以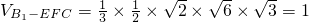 .
.点评:证明线面平行即在平面内找一条直线与已知直线平行;证明线线平行的方法有证明线面平行,中位线,平行四边形等方法,在这里运用了中位线也是我们常见的一种方法;求三棱锥的体积关键是找到合适的高与底面,即换一个顶点.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
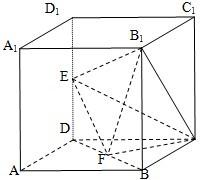 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1、DB的中点.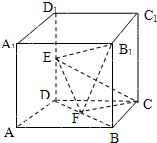 17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点
17、如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E,F分别为DD1,DB的中点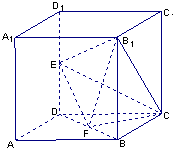 如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点.
如图所示,在棱长为2的正方体中,E、F分别为DD1、BD的中点. 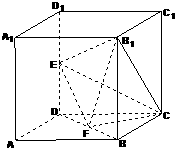 如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.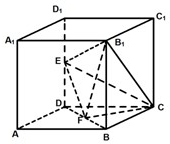 (2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.
(2012•虹口区三模)如图所示,在棱长为2的正方体ABCD-A1B1C1D1中,E、F分别为DD1、DB的中点.